Lineare Gleichungen: Unterschied zwischen den Versionen

Aus Wiki Herr Kimmig
Wechseln zu: Navigation, Suche
(→‎Erste Möglichkeit)
(→‎Summe zweier Gleichungen)
 
(4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 162: Zeile 162:
 
\end{matrix}</math>
 
\end{matrix}</math>
  
−
Die Lösungsmenge ist also <math>\mathbb L=\{3\}</math>
+
Die Lösungsmenge ist also <math>\mathbb L=\{3\}</math>.
  
 
==== Zweite Möglichkeit ====
 
==== Zweite Möglichkeit ====
 +
Bei der zweiten Möglichkeit bringen wir zuerst durch Subtraktion die Gleichungen auf eine Form, in welcher auf der linken Seite nur noch Terme mit und auf der rechten Seite alle Terme ohne <math>x</math> stehen bleiben:
 +
 +
<math>\begin{matrix}
 +
&2\cdot x+5&=&11&\qquad|\ -5\\
 +
\iff\quad &(2\cdot x+5)-5&=&(11)-5&\qquad|\ \text{Klammern auflösen}\\
 +
\iff\quad &2\cdot x+5-5&=&11-5&\qquad|\ \text{zusammenfassen}\\
 +
\iff\quad &2\cdot x&=&6
 +
\end{matrix}</math>
 +
 +
Jetzt können wir im zweiten Schritt <math>x</math> berechnen:
 +
 +
<math>\begin{matrix}
 +
&2\cdot x&=&6&\qquad|\ \div2\\
 +
\iff\quad &(2\cdot x)\div2&=&(6)\div2&\qquad|\ \text{Klammern auflösen}\\
 +
\iff\quad &2\cdot x\div2&=&6\div2&\qquad|\ \text{zusammenfassen}\\
 +
\iff\quad &x&=&3
 +
\end{matrix}</math>
 +
 +
Wir erhalten als Lösungsmenge also ebenfalls <math>\mathbb L=\{3\}</math>.
 +
 +
==== Fazit ====
 +
Welcher von den beiden Lösungswegen wir benutzen spielt für das Ergebnis keine Rolle. '''Oft''' (aber nicht immer) ist es einfacher, wenn wir die zweite Möglichkeit benutzen, d.h. zuerst die Gleichung zu "sortieren": alle Teile mit <math>x</math> auf die linke Seite, alle Teile ohne <math>x</math> auf die rechte Seite.
 +
 +
=== Beispiele für komplexere Gleichungen - Teil 2 ===
 +
Es kann auch vorkommen, dass in einer Gleichung die Unbekannte sogar auf beiden Seiten mit dabei steht. Neben einfachen Zahlen können wir auch die Variablen (wieder auf beiden Seiten der Gleichung) addieren bzw. subtrahieren, '''nicht jedoch multiplizieren/dividieren'''!
 +
 +
So können wir auch das obere "[[lineare Gleichungen#komplexeres Beispiel mit Wertetabelle|komplexere Beispiel mit Wertetabelle]]" berechnen:
 +
 +
<math>\begin{matrix}
 +
&2+3\cdot k&=&2\cdot k+6&\qquad|\ -2k\\
 +
\iff\quad &(2+3k)-2k&=&(2k+6)-2k&\qquad|\ \text{Klammern auflösen}\\
 +
\iff\quad &2+3k-2k&=&2k+6-2k&\qquad|\ \text{zusammenfassen}\\
 +
\iff\quad &2+1k&=&6&\qquad|\ -2\\
 +
\iff\quad &(2+k)-2&=&(6)-2&\qquad|\ \text{Klammern auflösen und zusammenfassen}\\
 +
\iff\quad &k&=&4
 +
\end{matrix}</math>
 +
 +
Und haben damit die Lösung <math>\mathbb L=\{4\}</math> auch rechnerisch gefunden.
 +
 +
== Summe zweier Gleichungen ==
 +
''Hinweis: dieser Abschnitt wird im Zusammenhang mit [[lineare Gleichungssysteme|linearen Gleichungssystemem]] relevant.''
 +
 +
Wie wir oben gesehen haben, dürfen wir bei einer Gleichung auf beiden Seiten den selben Wert addieren bzw. subtrahieren. Bei der Waage dürfen wir also auf beiden Seiten beispielsweise ein <math>2\,\mathrm{kg}</math>-Gewicht hinzufügen ohne dass sich am gesamten Gleichgewicht etwas ändert.
 +
 +
Es ist allerdings ebenfalls klar, dass wir auch auf einer Seite ''ein <math>2\,\mathrm{kg}</math>-Gewicht'', auf der anderen Seite beispielsweise ''zwei <math>1\,\mathrm{kg}</math>-Gewichte'' hinzufügen dürfen, da insgesamt ebenfalls wieder das selbe Gewicht auf beiden Seiten addiert wird. Das dürfen wir deshalb tun, da <math>2\,\mathrm{kg}=2\cdot1\,\mathrm{kg}</math> ist. Wir müssen also auf den beiden Seiten nicht unbedingt '''das Selbe''' hinzufügen (d.h. identische Gewichte), wir dürfen genausogut auch '''das Gleiche''' hinzufügen (d.h. lediglich der Gesamtwert auf beiden Seiten muss identisch sein, die Unterteilung spielt keine Rolle).
 +
 +
Bei einer '''Gleichung''' wissen wir aber, dass der Term auf der linken Seite '''das Gleiche''' ist, bzw. den gleichen Wert hat wie der Term auf der linken Seite.
 +
 +
Haben wir zwei zusammengehörige Gleichungen, so können wir mit dieser Überlegung beide Gleichungen ''zusammenaddieren''.
 +
 +
=== Beispiel mit Gewichten (ohne Variable) ===
 +
Wir nehmen die beiden Gleichungen
 +
 +
<math>\begin{matrix}
 +
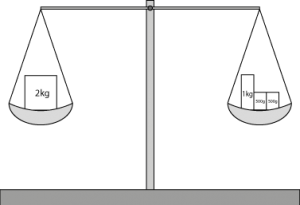
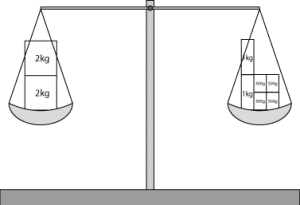
(I)\quad&2\cdot 1\,\mathrm{kg}&=&1\cdot2\,\mathrm{kg}\\
 +
(II)\quad&1\cdot 3\,\mathrm{kg}&=&2\cdot 1\,\mathrm{kg}+2\cdot0.5\,\mathrm{kg}
 +
\end{matrix}</math>
 +
 +
Hier wird es schnell klar, dass wir die Summe davon bilden können, indem wir die beiden linken Seiten addieren und ebenso die beiden rechten Seiten:
 +
 +
<math>\begin{matrix}
 +
(I)+(II)\quad&(\underbrace{2\cdot 1\,\mathrm{kg}}_{\text{aus Gleichung (I)}})+(\underbrace{1\cdot 3\,\mathrm{kg}}_{\text{aus Gleichung (II)}})&=&(\underbrace{1\cdot2\,\mathrm{kg}}_{\text{aus Gleichung (I)}})+(\underbrace{2\cdot 1\,\mathrm{kg}+2\cdot0.5\,\mathrm{kg}}_{\text{aus Gleichung (II)}})
 +
\end{matrix}</math>
 +
 +
=== Beispiel mit Variable ===
 +
Wir nehmen die beiden Gleichungen
 +
 +
<math>\begin{matrix}
 +
(I)\quad&3x-4&=&11\\
 +
(II)\quad&-2x+11&=&1
 +
\end{matrix}</math>
 +
 +
Hier dürfen wir wie bei den Gewichten die Summe aus beiden Gleichungen bilden:
 +
 +
<math>\begin{matrix}
 +
(I)+(II)\quad&(\underbrace{3x-4}_{\text{aus Gleichung (I)}})+(\underbrace{-2x+11}_{\text{aus Gleichung (II)}})&=&(\underbrace{11}_{\text{aus Gleichung (I)}})+(\underbrace{1}_{\text{aus Gleichung (II)}})&\qquad|\ \text{umstellen}\\
 +
\iff\quad&3x-2x-4+11&=&11+1&\qquad|\ \text{zusammenfassen}\\
 +
\iff\quad&x+7&=&12&\qquad|\ -7\\
 +
\iff\quad&x&=&5
 +
\end{matrix}</math>
 +
 +
=== Beispiel mit mehreren Variablen ===
 +
''Hinweis: dieser Abschnitt dient hier nur zur Verdeutlichung der Addition von verschiedenen Gleichungen und stellt keine Lösung dar! Für Lösungsverfahren von Gleichungen mit mehreren Variablen s. Kapitel [[lineare Gleichungssysteme]]''
 +
 +
Wir betrachten die beiden Gleichungen
 +
 +
<math>\begin{matrix}
 +
(I)\quad&3\square+4&=&2\bigcirc+5\\
 +
(II)\quad&-\bigcirc+4&=&2\square-6
 +
\end{matrix}</math>
 +
 +
(Variablen können nicht nur Buchstaben sein, sondern wie hier auch andere Zeichen oder Symbole!)
 +
 +
Wie oben addieren wir die beiden Gleichungen:
 +
 +
<math>\begin{matrix}
 +
(I)+(II)\quad&(\underbrace{3\square+4}_{\text{aus Gleichung (I)}})+(\underbrace{-\bigcirc+4}_{\text{aus Gleichung (II)}})&=&(\underbrace{2\bigcirc+5}_{\text{aus Gleichung (I)}})+(\underbrace{2\square-6}_{\text{aus Gleichung (II)}})&\qquad|\ \text{umstellen}\\
 +
\iff\quad&3\square-\bigcirc+8&=&2\square+2\bigcirc-1
 +
\end{matrix}</math>
 +
 +
Durch geschickte Addition zweier Gleichungen lässt sich erreichen, dass einige Variablen "herausfallen" und in der ''Summengleichung'' nicht mehr auftreten. Näheres siehe unter [[lineare Gleichungssysteme#Additionsverfahren|lineare Gleichungssysteme -> Additionsverfahren]].
 +
 +
== weitere Aufgaben ==
 +
* [[lineare Gleichungen - Aufgaben]]
 +
 +
== weitere Informationen ==
 +
* Äquivalenzumformungen: http://de.wikipedia.org/wiki/Äquivalenzumformung

Aktuelle Version vom 8. Juni 2015, 14:42 Uhr


Vorwissen

Term, Menge

Gleichungen

Viele Probleme des Alltags können mathematisch in einer Gleichung beschrieben und gelöst werden. Die wohl bekannteste Gleichung ist von Einstein: .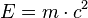

Gleichungen geben eine Beziehung zwischen zwei Termen an, und zwar dahingehend, dass die Terme auf beiden Seiten des Gleichzeichens den gleichen Wert annehmen.

Grundproblem

Gleichungen können wir dazu benutzen, um Lösungen für unbekannte Werte zu bestimmen. Als einfaches Beispiel betrachten wir die Gleichung

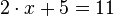
Welchen Wert müssen wir für einsetzen, damit die Gleichung stimmt?

Einfaches Beispiel mit Wertetabelle

Den richtigen Wert für können durch ausprobieren herausfinden. Hierfür verwenden wir für den Term auf der linken Seite eine Wertetabelle:

linke Seite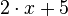
 rechte Seite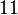
0 5 11
1 7 11
2 9 11
3 11 11
4 13 11
5 15 11
6 17 11

Wie wir jetzt in der Tabelle ablesen können, stimmen der Term 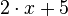(linke Seite) und der Term 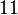(rechte Seite) gerade dann überein, wenn wir für den Wert 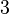einsetzen. Die Lösungsmenge der Gleichung ist also

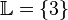
komplexeres Beispiel mit Wertetabelle

Auch Lösungen für komplexere Gleichungen, in denen die Variable auf beiden Seiten vorkommt, können wir mit einer Wertetabelle lösen. Betrachten wir hierfür die Gleichung

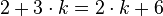
Wir stellen wieder die Wertetabelle auf:

linke Seite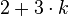
 rechte Seite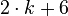
0 2 6
1 5 8
2 8 10
3 11 12
4 14 14
5 17 16
6 20 18

Die Gleichheit beider Seiten ist also gerade dann erfüllt, wenn wir für 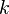den Wert 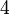einsetzen, Die Lösungsmenge ist also:

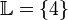
Äquivalenzumformungen

Das Lösen von Gleichungen mithilfe einer Wertetabelle funktioniert nur dann gut, wenn die Lösung ganzzahlig und recht klein ist. Anderenfalls ist dieser Lösungsweg sehr aufwändig. Besser wäre es, wenn wir die Lösung einer Gleichung direkt berechnen könnten.

Das Waagemodell

Balkenwaage im Gleichgewicht

Wir können uns eine Gleichung als Balkenwaage vorstellen. Damit diese ausgeglichen ist, müssen die Gegenstände auf beiden Seiten gleich schwer sein. Verändern wir etwas auf einer Seite, so müssen wir dieselbe Änderung auch auf der anderen Seite durchführen damit die Waage im Gleichgewicht bleibt.

Wir können beispielsweise auf beiden Seiten jeweils 1kg mehr dazu legen oder wegnehmen, dann bleibt die Waage trotzdem im Gleichgewicht.

Genauso können wir auch mit einer Gleichung verfahren: da wir wissen, dass die Terme auf beiden Seiten gleich sind bzw. das Gleiche beinhalten ist unsere "Gleichungswaage" ausgeglichen. Wir können jetzt auf beiden Seiten jeweils einen Wert hinzufügen (addieren) oder wegnehmen (subtrahieren) so dass die neue Gleichung äquivalent zur alten ist.

Äquivalent kommt aus dem lateinischen und setzt sich aus den Teilwörtern aequus (gleich) und valens (wertig) zusammen, und bedeutet also gleichwertig. Gleichwertige Gleichungen sind solche, die die selbe Lösungsmenge besitzen.

Addieren oder subtrahieren wir auf beiden Seiten den selben Wert, so ändert sich die Lösungsmenge nicht, die beiden Gleichungen sind also äquivalent. Man nennt so eine Umformung deshalb auch Äquivalenzumformung.

Beispiel mit Addition/Subtraktion

Wir betrachten die Gleichung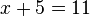

Subtrahieren wir auf beiden Seiten jeweils den Wert 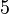so bekommen wir:

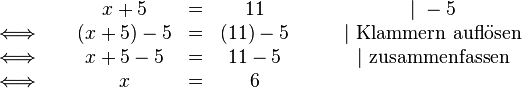
Die Lösungsmenge der Gleichung ist also

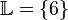
Hinweis: im Unterschied zu einer Waage, können in einer Gleichung auch negative Werte auftreten!

formelles

Um darzustellen, welche Umformung man zum nächsten Schritt durchführt gibt man hinter der Gleichung die jeweilige Aktion an. Vor die umgeformte Gleichung schreiben wir einen Aquivalenzpfeil 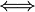um anzugeben, dass diese beiden Gleichungen äquivalent sind.

Vervielfachung

Verdopplung auf beiden Seiten (gegenüber dem ersten Bild, s.o.)

Neben dem Hinzufügen bzw. Wegnehmen von einem bestimmten Wert auf beiden Seiten, können wir das jeweilige Gewicht auf den beiden Seiten auch vervielfachen. Auch diese Tatsache wird anhand vom Waagenmodell sehr schnell klar: ist die Waage im Gleichgewicht, so sind also beide Seiten gleich schwer. Stellen wir auf beide Seiten der Waage nochmal das gleiche Gewicht so ändert sich die Waage nicht. Gleiches gilt auch umgekehrt, wenn wir das Gewicht auf beiden Seiten z.B. halbieren.

Mathematisch betrachtet können wir also beide Seiten mit dem selben Faktor multiplizieren, bzw. dividieren. Auch diese Umformung ist eine Äquivalenzumformung.

Beispiel mit Multiplikation/Division

Wir suchen die Lösung der Gleichung .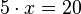

Dividieren wir beide Seiten durch 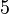so erhalten wir:

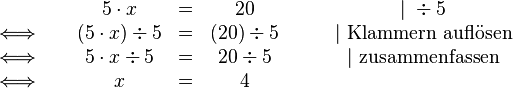
Die Lösungsmenge der Gleichung ist also

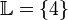
Wichtig: bei der Multiplikation bzw. Division ist es wichtig, die Klammern nicht zu vergessen! Im Beispiel würde es keinen Unterschied machen, jedoch werden wir im nächsten Abschnitt sehen, warum diese Klammern wichtig sind.

Beispiel für komplexere Gleichungen - Teil 1

Die meisten Gleichungen die wir haben können wir nicht nur durch Addition/Subtraktion oder Multiplikation/Division lösen, sondern müssen mehrere Schritte dafür berechnen. Wir schauen uns dazu noch einmal die erste Gleichung 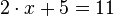an.

Überlegen wir zunächst, welches Ziel wir haben: Wir möchten den Wert für berechnen, für den die Gleichung "stimmt" (d.h. auf beiden Seiten der selbe Wert stehen bleibt). Gesucht ist also eine Gleichung .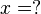

Wir müssen also unsere Ausgangsgleichung 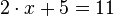durch Äquivalenzumfomungen schrittweise so umformen, dass am Ende auf der linken Seite nur noch und auf der rechten Seite eine Zahl (ohne ) stehen bleibt. Durch die vier Grundrechenarten können wir diese Gleichung schritt für Schritt umformen, wichtig hierbei ist nur, dass sämtliche Änderungen bzw. Rechenschritte auf beiden Seiten durchgeführt werden!

Erste Möglichkeit

Die erste Möglichkeit besteht darin, zuerst den Vorfaktor vor dem wegzubekommen. Hierfür müssen wir durch diesen Vorfaktor dividieren:

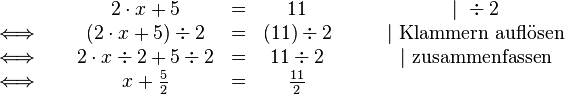
Hierbei sieht man auch, warum die Klammern wichtig sind, denn um die Klammern aufzulösen müssen wir das Distributivgesetz anwenden.

Im zweiten Schritt subtrahieren wir noch den zusätzlichen Wert, damit anschließend auf der linken Seite nur noch stehen bleibt:

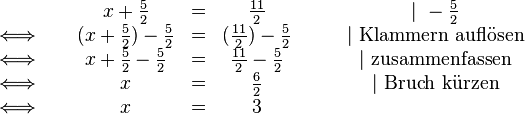
Die Lösungsmenge ist also .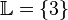

Zweite Möglichkeit

Bei der zweiten Möglichkeit bringen wir zuerst durch Subtraktion die Gleichungen auf eine Form, in welcher auf der linken Seite nur noch Terme mit und auf der rechten Seite alle Terme ohne stehen bleiben:

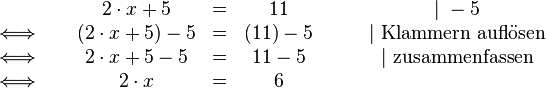
Jetzt können wir im zweiten Schritt berechnen:

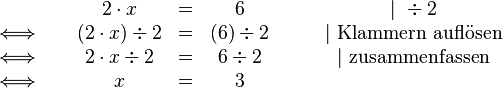
Wir erhalten als Lösungsmenge also ebenfalls .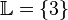

Fazit

Welcher von den beiden Lösungswegen wir benutzen spielt für das Ergebnis keine Rolle. Oft (aber nicht immer) ist es einfacher, wenn wir die zweite Möglichkeit benutzen, d.h. zuerst die Gleichung zu "sortieren": alle Teile mit auf die linke Seite, alle Teile ohne auf die rechte Seite.

Beispiele für komplexere Gleichungen - Teil 2

Es kann auch vorkommen, dass in einer Gleichung die Unbekannte sogar auf beiden Seiten mit dabei steht. Neben einfachen Zahlen können wir auch die Variablen (wieder auf beiden Seiten der Gleichung) addieren bzw. subtrahieren, nicht jedoch multiplizieren/dividieren!

So können wir auch das obere "komplexere Beispiel mit Wertetabelle" berechnen:

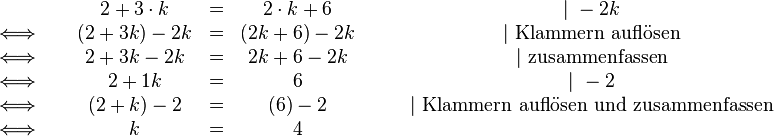
Und haben damit die Lösung 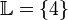auch rechnerisch gefunden.

Summe zweier Gleichungen

Hinweis: dieser Abschnitt wird im Zusammenhang mit linearen Gleichungssystemem relevant.

Wie wir oben gesehen haben, dürfen wir bei einer Gleichung auf beiden Seiten den selben Wert addieren bzw. subtrahieren. Bei der Waage dürfen wir also auf beiden Seiten beispielsweise ein 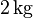-Gewicht hinzufügen ohne dass sich am gesamten Gleichgewicht etwas ändert.

Es ist allerdings ebenfalls klar, dass wir auch auf einer Seite ein 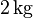-Gewicht, auf der anderen Seite beispielsweise zwei 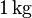-Gewichte hinzufügen dürfen, da insgesamt ebenfalls wieder das selbe Gewicht auf beiden Seiten addiert wird. Das dürfen wir deshalb tun, da 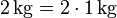ist. Wir müssen also auf den beiden Seiten nicht unbedingt das Selbe hinzufügen (d.h. identische Gewichte), wir dürfen genausogut auch das Gleiche hinzufügen (d.h. lediglich der Gesamtwert auf beiden Seiten muss identisch sein, die Unterteilung spielt keine Rolle).

Bei einer Gleichung wissen wir aber, dass der Term auf der linken Seite das Gleiche ist, bzw. den gleichen Wert hat wie der Term auf der linken Seite.

Haben wir zwei zusammengehörige Gleichungen, so können wir mit dieser Überlegung beide Gleichungen zusammenaddieren.

Beispiel mit Gewichten (ohne Variable)

Wir nehmen die beiden Gleichungen

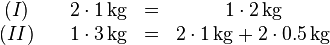
Hier wird es schnell klar, dass wir die Summe davon bilden können, indem wir die beiden linken Seiten addieren und ebenso die beiden rechten Seiten:

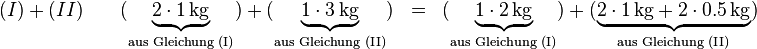
Beispiel mit Variable

Wir nehmen die beiden Gleichungen

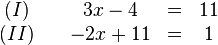
Hier dürfen wir wie bei den Gewichten die Summe aus beiden Gleichungen bilden:

Beispiel mit mehreren Variablen

Hinweis: dieser Abschnitt dient hier nur zur Verdeutlichung der Addition von verschiedenen Gleichungen und stellt keine Lösung dar! Für Lösungsverfahren von Gleichungen mit mehreren Variablen s. Kapitel lineare Gleichungssysteme

Wir betrachten die beiden Gleichungen

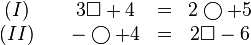
(Variablen können nicht nur Buchstaben sein, sondern wie hier auch andere Zeichen oder Symbole!)

Wie oben addieren wir die beiden Gleichungen:

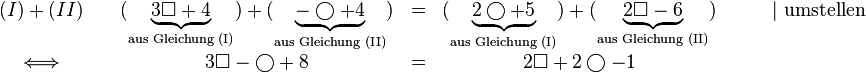
Durch geschickte Addition zweier Gleichungen lässt sich erreichen, dass einige Variablen "herausfallen" und in der Summengleichung nicht mehr auftreten. Näheres siehe unter lineare Gleichungssysteme -> Additionsverfahren.

weitere Aufgaben

weitere Informationen

Von „http://wiki.lehrer-kimmig.de/index.php?title=Lineare_Gleichungen&oldid=143“