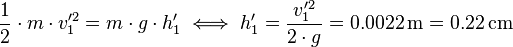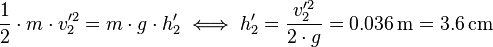Elastischer Stoß: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Aufgabe 2 == Ein Güterwaggon der Masse 25t rollt ein 50m langes, unter 2° gegen die Horizpntale geneigtes Gleis hinab und stößt dann auf einen dort abge…“) |
(→Definition) |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Aufgabe 2 == | + | == Vorwissen == |
| + | [[Impuls]], [[kinetische Energie]], [[Energieerhaltungssatz]] | ||
| + | |||
| + | == Definition == | ||
| + | '''Bei einem ''elastischen Stoß'' prallen zwei Körper aufeinander und trennen sich anschließend wieder. Nach dem Aufprall bewegen sie sich unabhängig voneinander weiter.''' | ||
| + | |||
| + | Es gelten dabei der [[Energieerhaltungssatz]] und der [[Impuls#Impulserhaltungssatz|Impulserhaltungssatz]] | ||
| + | |||
| + | === Beispiele === | ||
| + | Beispiele für einen elastischen Stoß sind: Billardkugeln, Newton-Pendel,... | ||
| + | |||
| + | == Beispielrechnung == | ||
| + | Gegeben sind zwei Kugeln der Masse <math>m_1=m_2=100\,\mathrm g</math>. Die erste Kugel prallt mit einer Geschwindigkeit von <math>v_1=0.50\,\frac{\mathrm m}{\mathrm s}</math> auf die zweite, ruhende Kugel (also <math>v_2=0\,\frac{\mathrm m}{\mathrm s}). Gesucht sind die beiden Geschwindigkeiten nach dem Stoß. | ||
| + | |||
| + | Es gilt der Impulserhaltungssatz: | ||
| + | |||
| + | <math>m_1v_1+m_2v_2=m_1v_1'+m_2v_2'</math> | ||
| + | |||
| + | sowie der Energieerhaltungssatz: | ||
| + | |||
| + | <math>\frac12m_1\cdot v_1^2+\frac12m_2\cdot v_2^2=\frac12m_1\cdot v_1'^2+\frac12m_2\cdot v_2'^2</math> | ||
| + | |||
| + | Setzt man die gegebenen Werte in den Impulserhaltungssatz ein und löst die Gleichung nach <math>v_1'</math> auf, so erhält man: | ||
| + | |||
| + | <math>v_1'=0.5\,\frac{\mathrm m}{\mathrm s}-v_2'</math> | ||
| + | |||
| + | Diesen Ausdruck kann man für <math>v_1'</math> in den Energieerhaltungssatz einsetzen und die dadurch entstandene Gleichung nach <math>v_2'</math> auflösen. Man erhält dabei mit der Mitternachtsformel: | ||
| + | |||
| + | <math>v_2'=0.5\,\frac{\mathrm m}{\mathrm s}</math> | ||
| + | |||
| + | und damit | ||
| + | |||
| + | <math>v_1'=0\,\frac{\mathrm m}{\mathrm s}</math> | ||
| + | |||
| + | == Direkte Formeln == | ||
| + | Um nicht bei jeder Aufgabe diese Umformungen durchführen zu müssen kann man diese auch allgemein berechnen und erhält daraus die beiden Formeln: | ||
| + | |||
| + | <math>v_1'=\frac{m_1v_1+m_2(2v_2-v_1)}{m_1+m_2}</math> | ||
| + | |||
| + | und | ||
| + | |||
| + | <math>v_2'=\frac{m_2v_2+m_1(2v_1-v_2)}{m_1+m_2}</math> | ||
| + | |||
| + | === Herleitung === | ||
| + | Die Herleitung dieser beiden Formeln ist etwas aufwändig. Sie wird deshalb nicht im Unterricht besprochen! | ||
| + | |||
| + | Zunächst löst man den Impulserhaltungssatz nach <math>v_1'</math> auf: | ||
| + | |||
| + | <math>m_1\cdot v_1+m_2\cdot v_2=m_1\cdot v_1'+m_2\cdot v_2'\iff v_1'=v_1+\frac{m_2}{m_1}\cdot(v_2-v_2')</math> | ||
| + | |||
| + | und setzt diesen Ausdruck in den Energieerhaltungssatz ein: | ||
| + | |||
| + | <math>\frac12m_1\cdot v_1^2+\frac12m_2\cdot v_2^2=\frac12m_1\cdot \Bigl(v_1+\frac{m_2}{m_1}\cdot(v_2-v_2')\Bigr)^2+\frac12m_2\cdot v_2'^2</math> | ||
| + | |||
| + | Um die weiteren Rechnungen zu vereinfachen können wir die Gesamte Gleichung mit <math>2</math> multiplizieren: | ||
| + | |||
| + | <math>m_1\cdot v_1^2+m_2\cdot v_2^2=m_1\cdot \Bigl(v_1+\frac{m_2}{m_1}\cdot(v_2-v_2')\Bigr)^2+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | Hier muss man zuerst die Klammer mithilfe der bionmischen Formel auflösen: | ||
| + | |||
| + | <math>m_1\cdot v_1^2+m_2\cdot v_2^2=m_1\cdot\underbrace{\Bigl(v_1+\frac{m_2}{m_1}\cdot(v_2-v_2')\Bigr)^2}_{=v_1^2+2\cdot v_1\cdot\frac{m_2}{m_1}\cdot(v_2-v_2')+\frac{m_2^2}{m_1^2}\cdot(v_2-v_2')^2}+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | <math>m_1\cdot v_1^2+m_2\cdot v_2^2=m_1\cdot\Bigl(v_1^2+2\cdot v_1\cdot\frac{m_2}{m_1}\cdot(v_2-v_2')+\frac{m_2^2}{m_1^2}\cdot\underbrace{(v_2-v_2')^2}_{=v_2^2-2\cdot v_2\cdot v_2'+v_2'^2}\Bigr)+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | <math>m_1\cdot v_1^2+m_2\cdot v_2^2=m_1\cdot\Bigl(v_1^2+2\cdot v_1\cdot\frac{m_2}{m_1}\cdot(v_2-v_2')+\frac{m_2^2}{m_1^2}\cdot(v_2^2-2\cdot v_2\cdot v_2'+v_2'^2)\Bigr)+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | <math>m_1\cdot v_1^2+m_2\cdot v_2^2=m_1\cdot v_1^2+2\cdot v_1\cdot m_2\cdot(v_2-v_2')+\frac{m_2^2}{m_1}\cdot(v_2^2-2\cdot v_2\cdot v_2'+v_2'^2)+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | <math>m_2\cdot v_2^2=2\cdot v_1\cdot m_2\cdot(v_2-v_2')+\frac{m_2^2}{m_1}\cdot(v_2^2-2\cdot v_2\cdot v_2'+v_2'^2)+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | <math>m_2\cdot v_2^=2\cdot v_1\cdot m_2\cdot v_2-2\cdot v_1\cdot m_2\cdot v_2'+\frac{m_2^2}{m_1}\cdot v_2^2-2\cdot \frac{m_2^2}{m_1}\cdot v_2\cdot v_2'+\frac{m_2^2}{m_1}\cdot v_2'^2+m_2\cdot v_2'^2</math> | ||
| + | |||
| + | Da wir hierdurch eine quadratische Gleichung für <math>v_2'</math> bekommen, die wir mithilfe der Mitternachtsformel lösen können, müssen wir die Anteile zunächst sortieren: | ||
| + | |||
| + | <math>v_2'^2\cdot\underbrace{\Bigl(m_2+\frac{m_2^2}{m_1}\Bigr)}_{=a}+v_2'\cdot\underbrace{\Bigl(-2v_1m_2-2\frac{m_2^2}{m_1}v_2\Bigr)}_{=b}+\underbrace{\Bigl(-m_2v_2^2+2v_1m_2v_2+\frac{m_2^2}{m_1}v_2^2\Bigr)}_{=c}=0</math> | ||
| + | |||
| + | Nun kann man diese Werte in die Mitternachtsformel einsetzen: | ||
| + | |||
| + | <math>{v_2'}_{1,2}=\frac{-\Bigl(-2v_1m_2-2\frac{m_2^2}{m_1}v_2\Bigr)\pm\sqrt{\Bigl(-2v_1m_2-2\frac{m_2^2}{m_1}v_2\Bigr)^2-4\cdot\Bigl(m_2+\frac{m_2^2}{m_1}\Bigr)\cdot\Bigl(-m_2v_2^2+2v_1m_2v_2+\frac{m_2^2}{m_1}v_2^2\Bigr)}}{2\cdot\Bigl(m_2+\frac{m_2^2}{m_1}\Bigr)}</math> | ||
| + | |||
| + | Betrachten wir zunächst die Diskriminante und vereinfachen diese: | ||
| + | |||
| + | <math>D=\Bigl(-2v_1m_2-2\frac{m_2^2}{m_1}v_2\Bigr)^2-4\cdot\Bigl(m_2+\frac{m_2^2}{m_1}\Bigr)\cdot\Bigl(-m_2v_2^2+2v_1m_2v_2+\frac{m_2^2}{m_1}v_2^2\Bigr)</math> | ||
| + | |||
| + | <math>D=4v_1^2m_2^2+8v_1v_2\frac{m_2^3}{m_1}+4\frac{m_2^4}{m_1^2}v_2^2-4\cdot\Bigl(-m_2^2v_2^2+2v_1m_2^2v_2+\frac{m_2^3}{m_1}v_2^2-\frac{m_2^3}{m_1}v_2^2+2v_1v_2\frac{m_2^3}{m_1}+\frac{m_2^4}{m_1^2}v_2^2\Bigr)</math> | ||
| + | |||
| + | <math>D=4v_1^2m_2^2+8v_1v_2\frac{m_2^3}{m_1}+4\frac{m_2^4}{m_1^2}v_2^2+4m_2^2v_2^2-8v_1m_2^2v_2-4\frac{m_2^3}{m_1}v_2^2+4\frac{m_2^3}{m_1}v_2^2-8v_1v_2\frac{m_2^3}{m_1}-4\frac{m_2^4}{m_1^2}v_2^2</math> | ||
| + | |||
| + | <math>D=4v_1^2m_2^2-8v_1m_2^2v_2+4m_2^2v_2^2</math> | ||
| + | |||
| + | <math>D=(2m_2v_1-2m_2v_2)^2</math> | ||
| + | |||
| + | Die gesamte Gleichung vereinfacht sich dadurch: | ||
| + | |||
| + | <math>{v_2'}_{1,2}=\frac{2m_2v_1+2\frac{m_2^2}{m_1}v_2\pm(2m_2v_1-2m_2v_2)}{2\cdot\Bigl(m_2+\frac{m_2^2}{m_1}\Bigr)}</math> | ||
| + | |||
| + | <math>{v_2'}_{1,2}=\frac{2\frac{m_2}{m_1}\cdot\bigl(m_1v_1+m_2v_2\pm(m_1v_1-m_1v_2)}{2\frac{m_2}{m_1}\cdot(m_1+m_2)\bigr)}</math> | ||
| + | |||
| + | <math>{v_2'}_{1,2}=\frac{m_1v_1+m_2v_2\pm(m_1v_1-m_1v_2)}{m_1+m_2}</math> | ||
| + | |||
| + | Rechnen wir hierbei für das <math>\pm</math> mit <math>-</math>, so erhalten wir die Gleichung <math>v_2'=v_2</math>. Diese Lösung macht also keinen Sinn, da dies die Geschwindigkeit ''direkt vor'' dem Stoß angibt. Es bleibt also als einzige mögliche Lösung die Rechnung mit <math>+</math>: | ||
| + | |||
| + | <math>v_2'=\frac{m_1v_1+m_2v_2+m_1v_1-m_1v_2}{m_1+m_2}</math> | ||
| + | |||
| + | <math>v_2'=\frac{m_2v_2+2m_1v_1-m_1v_2}{m_1+m_2}</math> | ||
| + | |||
| + | <math>v_2'=\frac{m_2v_2+m_1\cdot(2v_1-v_2)}{m_1+m_2}</math> | ||
| + | |||
| + | Damit erhalten wir die einfache, direkte Lösung für <math>v_2'</math>. Setzen wir diese in unsere Gleichung für <math>v_1'</math> ein, so erhalten wir auch hierfür eine einfache Gleichung: | ||
| + | |||
| + | <math>v_1'=v_1+\frac{m_2}{m_1}\cdot(v_2-v_2')</math> | ||
| + | |||
| + | <math>v_1'=v_1+\frac{m_2}{m_1}v_2-\frac{m_2}{m_1}\cdot\frac{m_2v_2+m_1\cdot(2v_1-v_2)}{m_1+m_2}</math> | ||
| + | |||
| + | <math>v_1'=\frac{(m_1+m_2)v_1}{m_1+m_2}+\frac{(m_1+m_2)\cdot\frac{m_2}{m_1}v_2}{m_1+m_2}-\frac{\frac{m_2}{m_1}\cdot\bigl(m_2v_2+m_1\cdot(2v_1-v_2)\bigr)}{m_1+m_2}</math> | ||
| + | |||
| + | <math>v_1'=\frac{m_1v_1+m_2v_1+m_2v_2+\frac{m_2^2}{m_1}v_2-\frac{m_2^2}{m_1}v_2-2m_2v_1+m_2v_2}{m_1+m_2}</math> | ||
| + | |||
| + | <math>v_1'=\frac{m_1v_1+2m_2v_2-m_2v_1}{m_1+m_2}</math> | ||
| + | |||
| + | <math>v_1'=\frac{m_1v_1+m_2(2v_2-v_1)}{m_1+m_2}</math> | ||
| + | |||
| + | == Übungsaufgaben == | ||
| + | === Aufgabe 1 === | ||
Ein Güterwaggon der Masse 25t rollt ein 50m langes, unter 2° gegen die Horizpntale geneigtes Gleis hinab und stößt dann auf einen dort abgestelltes, ruhenden Güterwaggon der Masse 18t. | Ein Güterwaggon der Masse 25t rollt ein 50m langes, unter 2° gegen die Horizpntale geneigtes Gleis hinab und stößt dann auf einen dort abgestelltes, ruhenden Güterwaggon der Masse 18t. | ||
| Zeile 30: | Zeile 153: | ||
Antwort: Der erste Waggon fährt nach dem Stoß mit einer Geschwindigkeit von <math>0.91\,\frac{\mathrm m}{\mathrm s}</math>, der zweite Waggon mit <math>6.5\,\frac{\mathrm m}{\mathrm s}</math> | Antwort: Der erste Waggon fährt nach dem Stoß mit einer Geschwindigkeit von <math>0.91\,\frac{\mathrm m}{\mathrm s}</math>, der zweite Waggon mit <math>6.5\,\frac{\mathrm m}{\mathrm s}</math> | ||
| − | == Aufgabe | + | === Aufgabe 2 === |
Ein Körper der Masse <math>m_1=2\,\mathrm{kg}</math> und der Geschwindigkeit <math>v_1=24\,\frac{\mathrm{km}}{\mathrm h}</math> trifft auf einen zweiten, | Ein Körper der Masse <math>m_1=2\,\mathrm{kg}</math> und der Geschwindigkeit <math>v_1=24\,\frac{\mathrm{km}}{\mathrm h}</math> trifft auf einen zweiten, | ||
ruhenden Körper der Masse <math>m_2</math>. Nach dem Stoß bewegen sich beide Körper mit gleich großer, aber entgegengesetzt gerichteter Geschwindigkeit voneinander weg. Wie groß ist die Masse <math>m_2</math> des zweiten Körpers und wie groß die Geschwindigkeiten nach dem Stoß? | ruhenden Körper der Masse <math>m_2</math>. Nach dem Stoß bewegen sich beide Körper mit gleich großer, aber entgegengesetzt gerichteter Geschwindigkeit voneinander weg. Wie groß ist die Masse <math>m_2</math> des zweiten Körpers und wie groß die Geschwindigkeiten nach dem Stoß? | ||
| Zeile 62: | Zeile 185: | ||
Damit ergibt sich <math>v_1'=-3.4\,\frac{\mathrm m}{\mathrm s}</math> und <math>v_2'=3.4\,\frac{\mathrm m}{\mathrm s}</math> | Damit ergibt sich <math>v_1'=-3.4\,\frac{\mathrm m}{\mathrm s}</math> und <math>v_2'=3.4\,\frac{\mathrm m}{\mathrm s}</math> | ||
| − | == Aufgabe | + | === Aufgabe 3 === |
Von zwei in gleicher Höhe pendelnd aufgehängten elastischen Kugeln ist die eine doppelt so schwer (<math>m_1=100\,\mathrm{g}</math>) wie die andere. Die schwerere Kugel wird um die Höhe <math>h=2\,\mathrm{cm}</math> angehoben und losgelassen. Welche Höhe <math>h_1'</math> und <math>h_2'</math> erreichen die Kugeln nach dem Zusammenprall? | Von zwei in gleicher Höhe pendelnd aufgehängten elastischen Kugeln ist die eine doppelt so schwer (<math>m_1=100\,\mathrm{g}</math>) wie die andere. Die schwerere Kugel wird um die Höhe <math>h=2\,\mathrm{cm}</math> angehoben und losgelassen. Welche Höhe <math>h_1'</math> und <math>h_2'</math> erreichen die Kugeln nach dem Zusammenprall? | ||
Aktuelle Version vom 24. Januar 2016, 21:46 Uhr
Inhaltsverzeichnis
Vorwissen
Impuls, kinetische Energie, Energieerhaltungssatz
Definition
Bei einem elastischen Stoß prallen zwei Körper aufeinander und trennen sich anschließend wieder. Nach dem Aufprall bewegen sie sich unabhängig voneinander weiter.
Es gelten dabei der Energieerhaltungssatz und der Impulserhaltungssatz
Beispiele
Beispiele für einen elastischen Stoß sind: Billardkugeln, Newton-Pendel,...
Beispielrechnung
Gegeben sind zwei Kugeln der Masse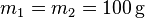 
. Die erste Kugel prallt mit einer Geschwindigkeit von 
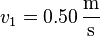auf die zweite, ruhende Kugel (also Fehler beim Parsen (Lexikalischer Fehler):
sowie der Energieerhaltungssatz:
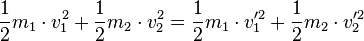
Setzt man die gegebenen Werte in den Impulserhaltungssatz ein und löst die Gleichung nach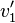 
auf, so erhält man:
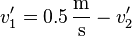
Diesen Ausdruck kann man für 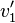in den Energieerhaltungssatz einsetzen und die dadurch entstandene Gleichung nach 
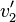auflösen. Man erhält dabei mit der Mitternachtsformel:
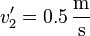
und damit
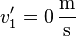
Direkte Formeln
Um nicht bei jeder Aufgabe diese Umformungen durchführen zu müssen kann man diese auch allgemein berechnen und erhält daraus die beiden Formeln:
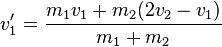
und
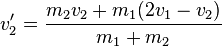
Herleitung
Die Herleitung dieser beiden Formeln ist etwas aufwändig. Sie wird deshalb nicht im Unterricht besprochen!
Zunächst löst man den Impulserhaltungssatz nach 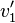auf:
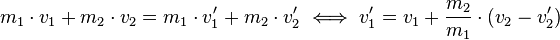
und setzt diesen Ausdruck in den Energieerhaltungssatz ein:
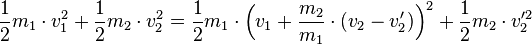
Um die weiteren Rechnungen zu vereinfachen können wir die Gesamte Gleichung mit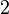 
multiplizieren:
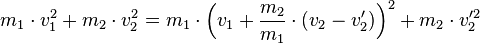
Hier muss man zuerst die Klammer mithilfe der bionmischen Formel auflösen:
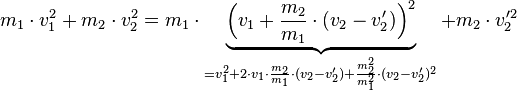
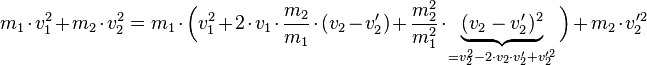
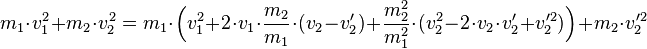
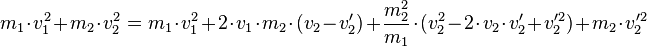
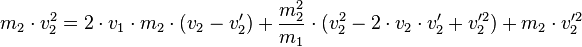
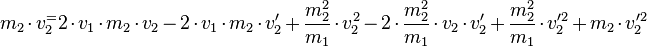
Da wir hierdurch eine quadratische Gleichung für 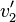bekommen, die wir mithilfe der Mitternachtsformel lösen können, müssen wir die Anteile zunächst sortieren:
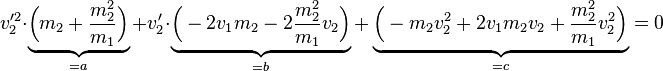
Nun kann man diese Werte in die Mitternachtsformel einsetzen:
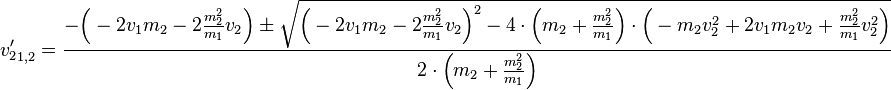
Betrachten wir zunächst die Diskriminante und vereinfachen diese:
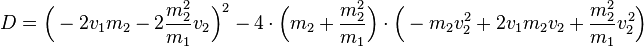
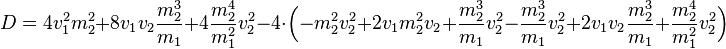
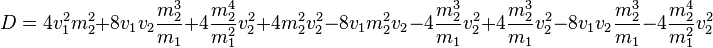
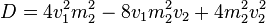
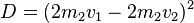
Die gesamte Gleichung vereinfacht sich dadurch:
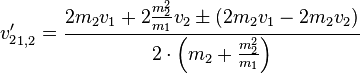
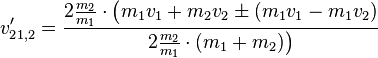
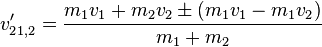
Rechnen wir hierbei für das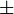 
mit 
, so erhalten wir die Gleichung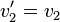 
. Diese Lösung macht also keinen Sinn, da dies die Geschwindigkeit direkt vor dem Stoß angibt. Es bleibt also als einzige mögliche Lösung die Rechnung mit 
:
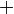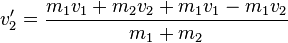
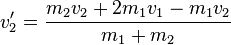
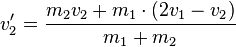
Damit erhalten wir die einfache, direkte Lösung für 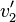. Setzen wir diese in unsere Gleichung für 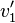ein, so erhalten wir auch hierfür eine einfache Gleichung:
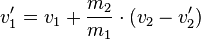
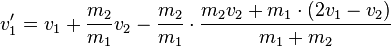
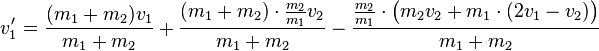
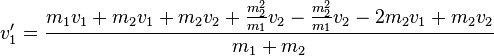
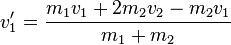
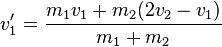
Übungsaufgaben
Aufgabe 1
Ein Güterwaggon der Masse 25t rollt ein 50m langes, unter 2° gegen die Horizpntale geneigtes Gleis hinab und stößt dann auf einen dort abgestelltes, ruhenden Güterwaggon der Masse 18t.
Mit welcher Geschwindigkeit stößt der erste Waggon an den zweiten?
Gegeben: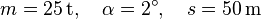 
Gesucht: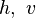 
Dazu berechnen wir zunächst die Gesamthöhe, die der Waggon aus potenzieller Energie in Bewegungsenergie umwandelt.
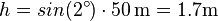
Mit dem Energieerhaltungssatz können wir nun die Geschwindigkeit berechnen:
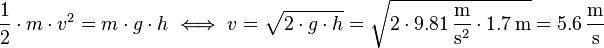
Antwort: Der erste Güterwaggon trifft mit einer Geschwindigkeit von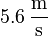 
auf den Zweiten.
Mit welcher Geschwindigkeit rollen die beiden Waggons weiter?
Gegeben: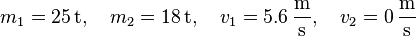 
Gesucht: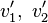 
physikalischer Zusammenhang: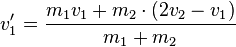 
und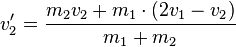
Einsetzen ergibt: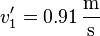 
und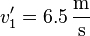 
Antwort: Der erste Waggon fährt nach dem Stoß mit einer Geschwindigkeit von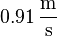 
, der zweite Waggon mit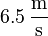 
Aufgabe 2
Ein Körper der Masse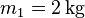 
und der Geschwindigkeit 
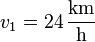trifft auf einen zweiten,
ruhenden Körper der Masse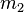 
. Nach dem Stoß bewegen sich beide Körper mit gleich großer, aber entgegengesetzt gerichteter Geschwindigkeit voneinander weg. Wie groß ist die Masse 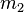des zweiten Körpers und wie groß die Geschwindigkeiten nach dem Stoß?
Gegeben: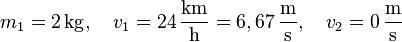 
, außerdem gilt die Bedingung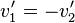 
Gesucht: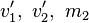 
physikalischer Zusammenhang: 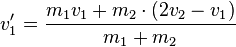und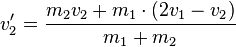
Aus der Bedingung 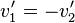folgt also:
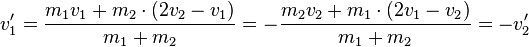
Also:
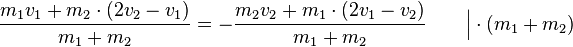
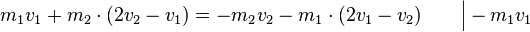
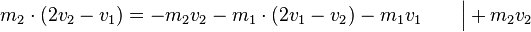
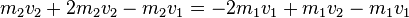
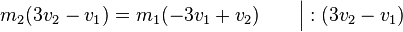
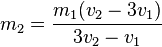
Einsetzen ergibt: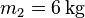 
Damit ergibt sich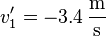 
und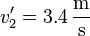 
Aufgabe 3
Von zwei in gleicher Höhe pendelnd aufgehängten elastischen Kugeln ist die eine doppelt so schwer (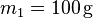
) wie die andere. Die schwerere Kugel wird um die Höhe 
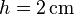angehoben und losgelassen. Welche Höhe 
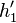und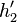 
erreichen die Kugeln nach dem Zusammenprall?
Gegeben: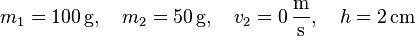 
Gesucht: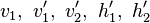 
Berechne zunächst mit dem Energieerhaltungssatz die Aufprallgeschwindigkeit:
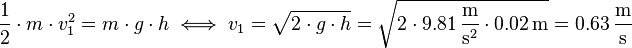
Anschließend können die Geschwindigkeiten nach dem Stoß berechnet werden:
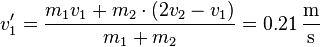
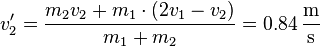
Damit können widerum mit dem Energieerhaltungssatz berechnet werden, welche Höhe die beiden Kugeln erreichen:
