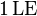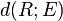Hesse'sche Normalenform: Unterschied zwischen den Versionen
(→Beispiel) |
(→Vorwissen) |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Category:Mathematik]] | ||
| + | [[Category:J1]] | ||
| + | |||
== Vorwissen == | == Vorwissen == | ||
| − | [[ | + | [[Vektoren]], [[Skalarprodukt]], [[Geraden im Raum]], [[Ebenen im Raum]], [[Normalenvektor]] [[Schnittpunkt Gerade-Ebene]], [[Abstand Punkt-Ebene]] |
== Problem == | == Problem == | ||
| Zeile 132: | Zeile 135: | ||
& = & \frac{10}3 | & = & \frac{10}3 | ||
\end{matrix}</math> | \end{matrix}</math> | ||
| + | |||
| + | == Hesse-Koordinatenform == | ||
| + | Den Abstand zwischen einer Ebene in Koordinatenform <math>E:\qquad a_1x_1+a_2x_2+a_3x_3=b</math> und einem Punkt <math>R(r_1\mid r_2\mid r_3)</math> können wir mit dieser Formel zwar berechnen, allerdings sind dazu folgende Schritte nötig: | ||
| + | # Bestimmung von <math>\vec n</math> und daraus <math>\vec{n_0}</math> | ||
| + | # Bestimmung eines beliebigen Punktes <math>P</math> auf der Ebene | ||
| + | # Aufstellen der Hesse'schen Normalenform | ||
| + | # Berechnung des Abstandes mit dieser. | ||
| + | |||
| + | In diesem Abschnitt wollen wir die oben erarbeitete Formel noch einmal umstellen damit wir auch für Ebenen in Koordinatenform den Abstand zu einem Punkt direkt berechnen können. | ||
| + | |||
| + | === Voraussetzungen === | ||
| + | '''Gegeben:''' | ||
| + | * eine Ebene in Koordinatenform <math>E:\qquad a_1x_1+a_2x_2+a_3x_3=b</math> | ||
| + | * einen Punkt <math>R(r_1\mid r_2\mid r_3)</math> | ||
| + | |||
| + | '''Gesucht:''' | ||
| + | * <math>d(R;E)</math> | ||
| + | |||
| + | '''Wir wissen:''' | ||
| + | * <math>d=\Bigl|\bigl[\vec r-\vec p\bigr]\cdot\vec{n_0}\Bigr|</math> | ||
| + | |||
| + | === Berechnung === | ||
| + | Wir wählen uns zuerst einen beliebigen Punkt <math>P</math> auf der Ebene mit den Koordinaten <math>P(p_1,p_2,p_3)</math>. Außerdem können wir den Normalenvektor direkt aus der Koordinatenform ablesen (s. [[M:Ebenen im Raum|Ebenen im Raum]]). Daraus bilden wir den Normaleneinheitsvektor | ||
| + | |||
| + | <math>\vec{n_0}=\left(\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right)\cdot\frac1{\sqrt{a_1^2+a_2^2+a_3^2}}</math> | ||
| + | |||
| + | Alles zusammen können wir in die HNF einsetzen: | ||
| + | |||
| + | <math>d=\Biggl|\left[\left(\begin{matrix}r_1\\r_2\\r_3\end{matrix}\right)-\left(\begin{matrix}p_1\\p_2\\p_3\end{matrix}\right)\right]\cdot \left(\begin{matrix}a_1\\a_2\\a_3\end{matrix}\right)\cdot\frac1{\sqrt{a_1^2+a_2^2+a_3^2}}</math> | ||
| + | |||
| + | Daraus erhalten wir durch Subtraktion der Klammer und Bilden des Skalarproduktes | ||
| + | |||
| + | <math>d=\Bigl|\frac{(r_1-p_1)a_1+(r_2-p_2)a_2+(r_3-p_3)a_3}{\sqrt{a_1^2+a_2^2+a_3^2}}\Bigr|</math> | ||
| + | |||
| + | Wir stellen den Zähler um und wissen, da der Punkt <math>P</math> in der Ebene liegt, dass <math>a_1p_1+a_2p_2+a_3p_3=b</math> gilt: | ||
| + | |||
| + | <math>d=\Bigl|\frac{r_1a_1+r_2a_2+r_3a_3-\overbrace{(p_1a_1+p_2a_2+p_3a_3)}^{=b}}{\sqrt{a_1^2+a_2^2+a_3^2}}\Bigr|</math> | ||
| + | |||
| + | Somit haben wir eine Formel in Koordinatenform erhalten, um den Abstand zwischen der Ebene und einem Punkt direkt zu berechnen: | ||
| + | |||
| + | <math>d=\Bigl|\frac{r_1a_1+r_2a_2+r_3a_3-b}{\sqrt{a_1^2+a_2^2+a_3^2}}\Bigr|</math> | ||
| + | |||
| + | === Beispiel === | ||
| + | Wie groß ist der Abstand zwischen der Ebene <math>E:\qquad x_1+2x_2+2x_3=-6</math> und dem Punkt <math>R(-3\mid1\mid-4)</math>? | ||
| + | |||
| + | Wir setzen in obere Formel ein: | ||
| + | <math>d=\Bigl|\frac{(-3)\cdot(1)+(1)\cdot(2)+(-4)\cdot(2)-(-6)}{\sqrt{1^2+2^2+2^2}}\Bigr|=\Bigl|\frac{-3+2-8+6}{\sqrt{9}}\Bigr|=\Bigl|\frac{-3}{3}\Bigr|=1</math> | ||
| + | |||
| + | Der Abstand zwischen <math>E</math> und <math>R</math> ist also <math>1\,\mathrm{LE}</math> | ||
| + | |||
| + | == Aufgaben == | ||
| + | * [[Hesse'sche Normalenform - Aufgaben]] | ||
Aktuelle Version vom 19. Mai 2015, 10:28 Uhr
Inhaltsverzeichnis
Vorwissen
Vektoren, Skalarprodukt, Geraden im Raum, Ebenen im Raum, Normalenvektor Schnittpunkt Gerade-Ebene, Abstand Punkt-Ebene
Problem
Wir haben eine Ebene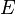 
im Raum und einen Punkt 
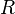, welcher nicht in der Ebene liegt. Um den Abstand zu berechnen müssen wir folgende Schritte durchführen bzw. berechnen:
- Bestimme den Normalenvektor
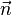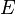
von - Berechne Gerade
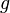durch Punkt 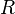mit Richtungsvektor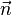 - Berechne den Schnittpunkt
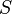zwischen der Geraden 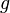und der Ebene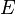 - Berechne den Abstand
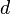zwischen den Punkten 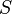und 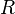, welcher gleichzeitig auch der Abstand vom Punkt 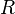zur Ebene 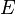angibt.
(s. auch Abstand Punkt-Ebene)
Es kann recht aufwändig sein, manuell den Schnittpunkt zwischen 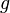und 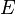zu berechnen. Wir suchen deshalb eine schnellere Methode, den Abstand zu berechnen.
Voraussetzung
Wir gehen davon aus, dass wir die Ebene in Koordinatenform
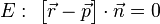
bereits angegeben haben, d.h. wir den Normalenvektor 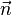direkt ablesen können. (Ansonsten können wir diesen auch durch Umrechnungen z.B. aus der Parameterform berechnen, s. Ebenen im Raum)
Für die Ebenengleichung spielt die Länge des Normalenvektors 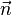keine Rolle, wir können deshalb für die weiteren Rechnungen annehmen, dass dieser die Länge 1 hat. wir bezeichnen einen solchen Vektor auch als Einheitsvektor, oder in diesem speziellen Fall auch Normaleneinheitsvektor 
.
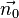Die Hesse'sche Normalenform
Eine Ebenengleichung in Normalenform bei welcher der Normalenvektor ein Einheitsvektor ist nennt man Hesse'sche Normalenform (kurz HNF), benannt nach Ludwig Otto Hesse:
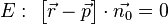
Diese gilt (wie bei der Normalenform) für alle Punkte 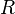(mit dem Ortsvektor 
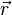) die in der Ebene liegen.
Diese Form bringt uns aber einen weiteren Vorteil: wir können damit den Abstand eines Punktes zu der Ebene bestimmen.
Bestimmung Abstand Punkt-Ebene mit der HNF
Für die nachfolgende Rechnung gilt:
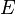- : Ebene mit HNF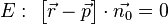
-
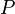: Stützpunkt der Ebene mit Ortsvektor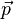 
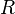- : Punkt außehalb der Ebene mit Ortsvektor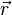
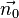- : Normaleneinheitsvektor der Ebene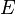
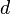- : Abstand zwischen Punkt 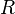und Ebene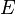
Behauptung
Für den Abstand 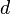gilt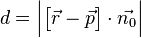 
Beweis
Für den Beweis können die einzelnen Schritte in GeoGebra grafisch nachverfolgt werden indem im oberen Bereich der Schieberegler eingestellt wird.
Schritt 1: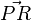 
Wir beginnen zunächst mit dem Term
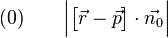
und formen diesen zuerst um, denn wir können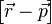 
durch den Vektor 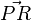ersetzen und wir erhalten daraus:
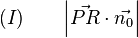
Schritt 2: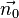
Für die weitere Betrachtung benötigen wir zusätzlich den Normaleneinheitsvektor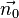
Schritt 3: Zerlegung von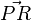
Nach der Vektoraddition erhalten wir bei der Addition zweier Vektoren wieder einen Vektor. Umgekehrt können wir einen Vektor auch in mehrere Vektoren zerlegen.
Wir zerlegen den Vektor 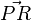in zwei Teile:
-
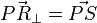: Ein Teil senkrecht zum Normalenvektor -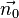
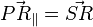: Ein Teil parallel zum Normalenvektor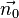
Für die Zeichnung brauchen wir hierfür noch den Punkt 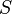. Wo dieser Punkt genau liegt benötigen wir für die weitere Rechnung nicht! Da wir aber wissen, dass 
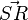wie der Normalenvektor ebenfalls senkrecht zur Ebene steht, schließen wir daraus direkt, dass 
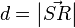gilt.
Mit dieser Zerlegung können wir den oberen Term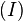 
weiter umschreiben:
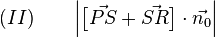
Mithilfe des Distributivgesetzes, welches auch für das Skalarprodukt gilt, bekommen wir
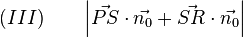
Weiter gilt für das Skalarprodukt, dass dieses für rechtwinklige Vektoren gerade 0 ergibt. Da wir den Vektor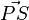 
gerade so gewählt haben, dass dieser orthogonal zum Normalenvektor ist, ergibt das Skalarprodukt 
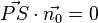. Das vereinfacht unseren Term 
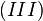weiter:
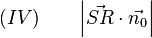
Schritt 4: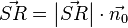 
Der Vektor 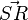ist parallel zum Normalenvektor 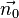. Alle parallelen Vektoren können wir schreiben als Produkt eines einzigen Vektores mit einem Streckungsfaktor.
Da wir einen Normaleneinheitsvektor der Länge 1 betrachten müssen wir diesen lediglich mit der Länge des Vektors 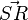multiplizieren um eben diesen zu erhalten. Daher gilt eben:
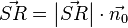
Achtung: Die Vektoren 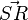und 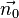können auch antiparallel sein! Das bedeutet, es könnte auch 
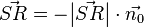gelten. Dies ist der Grund, warum wir stets den Betrag nehmen müssen.
Diesen Zusammenhang können wir nun in den Term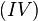 
einsetzen und erhalten:
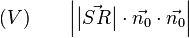
Für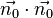 
gilt, wie für jeden Vektor: 
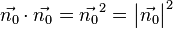. Da aber die Länge des Vektors 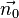gerade 1 ist, ist auch 
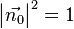. Deshalb vereinfacht sich der Term 
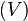zu
Aus Schritt 3 wissen wir, dass dieser Wert gerade dem Abstand 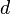entspricht. Hätten wir keinen Einheitsvektor, sondern einen Normalenvektor beliebiger Länge, so müssten wir das Ergebnis an dieser Stelle nochmals durch das Quadrat der Länge teilen (da 
)
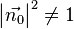Abschluss
Wir haben den Term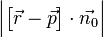 
in mehreren Schritten so umgeformt, dass wir als Ergebnis den Abstand 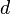bekommen haben. Wir können deshalb schreiben und sehen die Behauptung:
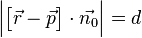
Beispiel
Es ist die Ebene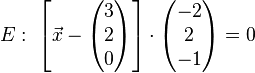 
und der Punkt 
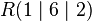gegeben. Wie groß ist der Abstand zwischen Punkt und Ebene?
Um den Abstand mit der HNF zu berechnen müssen wir die Ebene zuerst in diese HNF umformen. Da die Ebene bereits in Normalenform angegeben ist müssen wir lediglich den Normalenvektor der Länge 1 berechnen. Diesen bekommen wir durch Normalisierung des Normalenvektors. Hierfür multiplizieren wir diesen mit dem Kehrwert seiner Länge:
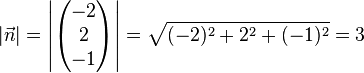
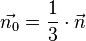
Also ist die Hesse'sche Normalenform:
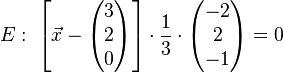
Den Abstand zum Punkt 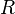bekommen wir nun einfach, indem wir dessen Ortsvektor für 
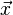einsetzen:
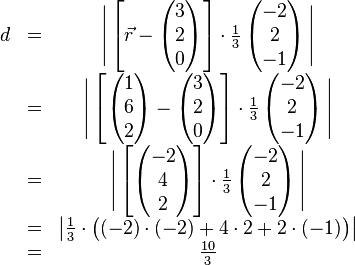
Hesse-Koordinatenform
Den Abstand zwischen einer Ebene in Koordinatenform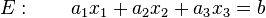 
und einem Punkt 
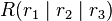können wir mit dieser Formel zwar berechnen, allerdings sind dazu folgende Schritte nötig:
- Bestimmung von 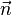und daraus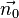
- Bestimmung eines beliebigen Punktes 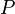auf der Ebene
- Aufstellen der Hesse'schen Normalenform
- Berechnung des Abstandes mit dieser.
In diesem Abschnitt wollen wir die oben erarbeitete Formel noch einmal umstellen damit wir auch für Ebenen in Koordinatenform den Abstand zu einem Punkt direkt berechnen können.
Voraussetzungen
Gegeben:
- eine Ebene in Koordinatenform
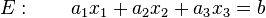
- einen Punkt
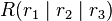
Gesucht:
Wir wissen:
Berechnung
Wir wählen uns zuerst einen beliebigen Punkt 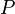auf der Ebene mit den Koordinaten 
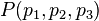. Außerdem können wir den Normalenvektor direkt aus der Koordinatenform ablesen (s. Ebenen im Raum). Daraus bilden wir den Normaleneinheitsvektor
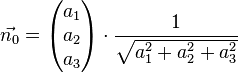
Alles zusammen können wir in die HNF einsetzen:
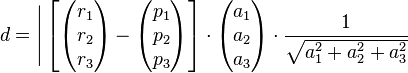
Daraus erhalten wir durch Subtraktion der Klammer und Bilden des Skalarproduktes
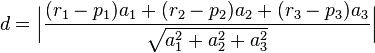
Wir stellen den Zähler um und wissen, da der Punkt 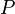in der Ebene liegt, dass 
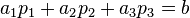gilt:
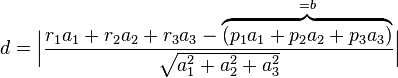
Somit haben wir eine Formel in Koordinatenform erhalten, um den Abstand zwischen der Ebene und einem Punkt direkt zu berechnen:
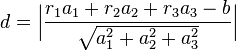
Beispiel
Wie groß ist der Abstand zwischen der Ebene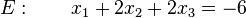 
und dem Punkt 
?
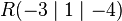Wir setzen in obere Formel ein:
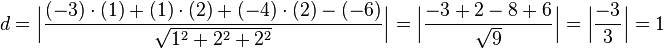
Der Abstand zwischen 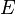und 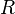ist also 
