Hesse'sche Normalenform - Aufgaben: Unterschied zwischen den Versionen
Aus Wiki Herr Kimmig
(Die Seite wurde neu angelegt: „== Aufgaben in Normalenform == === gegeben: Ebene in Normalenform und Punkt === berechne den Abstand vom Punkt <math>R</math> zur Ebene <math>E</math>: # <ma…“) |
(→gegeben: Ebene in Normalenform und Punkt) |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Category:Mathematik]] | ||
| + | [[Category:Aufgaben]] | ||
| + | |||
== Aufgaben in Normalenform == | == Aufgaben in Normalenform == | ||
| Zeile 5: | Zeile 8: | ||
# <math>E:\qquad \left[\vec x-\left(\begin{matrix}3\\2\\0\end{matrix}\right)\right]\cdot\left(\begin{matrix}2\\-2\\1\end{matrix}\right)</math>, <math>R(1\mid6\mid2)</math> | # <math>E:\qquad \left[\vec x-\left(\begin{matrix}3\\2\\0\end{matrix}\right)\right]\cdot\left(\begin{matrix}2\\-2\\1\end{matrix}\right)</math>, <math>R(1\mid6\mid2)</math> | ||
| + | #* Lösung: <math>d=\frac{10}{3}\,\mathrm{LE}</math> | ||
| + | # <math>E:\qquad \left[\vec x-\left(\begin{matrix}3\\1\\-1\end{matrix}\right)\right]\cdot\left(\begin{matrix}7\\-4\\4\end{matrix}\right)</math>, <math>R(1\mid6\mid2)</math> | ||
| + | #* Lösung: <math>d=3\,\mathrm{LE}</math> | ||
| + | # <math>E:\qquad \left[\vec x-\left(\begin{matrix}2\\-5\\1\end{matrix}\right)\right]\cdot\left(\begin{matrix}1\\2\\2\end{matrix}\right)</math>, <math>R(1\mid6\mid2)</math> | ||
| + | #* Lösung: <math>d=1\,\mathrm{LE}</math> | ||
| + | # <math>E:\qquad \left[\vec x-\left(\begin{matrix}1\\1\\0\end{matrix}\right)\right]\cdot\left(\begin{matrix}-2\\2\\-1\end{matrix}\right)</math>, <math>R(5\mid-4\mid3)</math> | ||
| + | #* Lösung: <math>d=7\,\mathrm{LE}</math> | ||
Aktuelle Version vom 13. Mai 2015, 16:14 Uhr
Aufgaben in Normalenform
gegeben: Ebene in Normalenform und Punkt
berechne den Abstand vom Punkt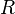 
zur Ebene 
:
-
, 
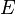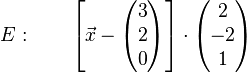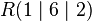
- Lösung:
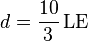
- Lösung:
-
,
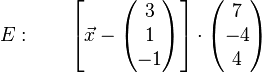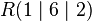
- Lösung:
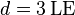
- Lösung:
-
,
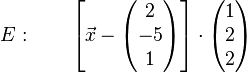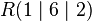
- Lösung:
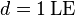
- Lösung:
-
, 
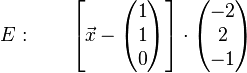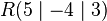
- Lösung:
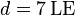
- Lösung:
