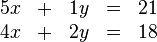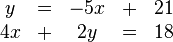Lineare Gleichungssysteme: Unterschied zwischen den Versionen
(→Einsetzungsverfahren) |
|||
| Zeile 54: | Zeile 54: | ||
Im Gegensatz zur grafischen Lösung versuchen wir hier rein mathematisch durch Berechnung auf das Ergebnis zu kommen. | Im Gegensatz zur grafischen Lösung versuchen wir hier rein mathematisch durch Berechnung auf das Ergebnis zu kommen. | ||
| − | Das Ziel dabei ist es, die beiden Gleichungen auf eine Gleichung zu reduzieren, in welche nur noch eine Unbekannte steht. Hierfür lösen wir eine | + | Das Ziel dabei ist es, die beiden Gleichungen auf eine Gleichung zu reduzieren, in welche nur noch eine Unbekannte steht. Hierfür lösen wir eine der beiden Gleichungen nach einer (geeigneten) Unbekannten um. Im Beispiel stellen wir die erste Gleichung nach <math>y</math> um: |
:<math>\begin{matrix} | :<math>\begin{matrix} | ||
y & = & -5x & + & 21\\ | y & = & -5x & + & 21\\ | ||
4x & + & 2y & = & 18 | 4x & + & 2y & = & 18 | ||
\end{matrix}</math> | \end{matrix}</math> | ||
| + | |||
| + | Da wir nun wissen, dass <math>y</math> identisch ist zu <math>-5x + 21</math> können wir eben dieses <math>y</math> in der zweiten Gleichung ersetzen und erhalten damit die Gleichung <math>4x + 2\cdot(-5x+21) = 18</math>. Nicht vergessen dürfen wir hier die Klammern! | ||
| + | |||
| + | Wir haben durch Umformen und Einsetzen also eine Gleichung erhalten, in der wir nur noch eine Unbekannte <math>x</math> haben. Diese können wir dann durch [[Äquivalenzumformungen]] lösen:<math>\begin{matrix} | ||
| + | 4x + 2\cdot(-5x+21) & = & 18 & \mid & \text{Klammer auflösen}\\ | ||
| + | 4x - 10x + 42 & = & 18 & \mid &-42\\ | ||
| + | -6x & = & -24 & \mid &\div-6 \\ | ||
| + | x & = & 4 | ||
| + | \end{matrix}</math> | ||
| + | |||
| + | Wir haben somit den Wert für <math>x</math> gefunden. | ||
| + | |||
| + | Um den noch fehlenden Wert für <math>y</math> berechnen zu können nehmen wir die oben umgestellte Gleichung <math>y = -5x + 21</math> und setzen den eben erhaltenen Wert von <math>x</math> ein:<math>\begin{matrix} | ||
| + | y & = & -5x & + & 21 & \mid & x=4\\ | ||
| + | y & = & -5\cdot 4 + 21 \\ | ||
| + | y & = & -20 + 21 \\ | ||
| + | y & = & 1 | ||
| + | \end{matrix}</math> | ||
| + | |||
| + | Somit haben wir auch über dieses Verfahren die Werte für <math>x</math> und <math>y</math> gefunden. | ||
| + | |||
| + | ==== Zusammenfassung ==== | ||
| + | ;Eine der Gleichungen umformen : <math>y=-5x+21</math> | ||
| + | ;Das Ergebnis in die zweite Gleichung einsetzen : <math>4x + 2\cdot(-5x+21) = 18</math> | ||
| + | ;Auflösen liefert Ergebnis für die erste Unbekannte : <math>x = 4</math> | ||
| + | ;In die zuerst umgeformte Gleichung einsetzen : <math>y=-5\cdot(4)+21</math> | ||
| + | ;Auflösen liefert Ergebnis für die zweite Unbekannte : <math>y=1</math> | ||
=== Gleichsetzungsverfahren === | === Gleichsetzungsverfahren === | ||
=== Additionsverfahren === | === Additionsverfahren === | ||
Version vom 5. Mai 2015, 09:27 Uhr
Inhaltsverzeichnis
Vorwissen
lineare Gleichungen, Äquivalenzumformungen
Grundproblem
Eine Gleichung mit nur einer Unbekannten können wir direkt lösen indem wir diese durch Äquivalenzumformungen umstellen. Sobald wir allerdings zwei oder mehr Unbekannte darin haben können wir diese nicht mehr direkt bestimmen.
Einstiegsproblem
von http://www.schule-studium.de/Mathe/Textaufgaben-Lineare-Gleichungssysteme.html
Herr Agricola hat einen kleinen landwirtschafltichen Betrieb mit Hühnern und Schweinen. Nach der Anzahl seiner Tiere gefragt, antwortet er: "Den Hund und die Katze mitgezählt, haben alle Tiere zusammen 89 Köpfe und 206 Beine."
Wie viele Hühner und Schweine hat Herr Agricola also?
Lineare Gleichungssysteme
Ein lineares Gleichungssystem ist eine Menge von linearen Gleichungen mit mehreren Unbekannten die alle gleichzeitig erfüllt sein sollen.
vlg. http://de.wikipedia.org/wiki/Lineares_Gleichungssystem
Beispiel
Wir haben die zwei Unbekannten 
und 
und 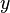die dazugehörigen Gleichungen
Wie müssen wir und 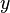wählen, so dass beide Gleichungen stimmen?
Lösungsverfahren
grafische Lösung
Jede Gleichung mit zwei Unbekannten lässt sich durch Umformung als lineare Funktion in einem Schaubild darstellen.
Zur grafischen Lösung des Linearen Gleichungssystems (LGS) müssen wir deshalb:
- zuerst die beiden Gleichungen nach 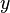auflösen/umformen
- die Schaubilder zeichnen
- grafisch den Schnittpunkt finden
- dessen Koordinaten ist die Lösung des LGS
- Erste Gleichung nach 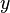umstellen
-
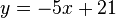
- Zweite Gleichung nach 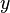umstellen
-
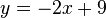
- Den Schnittpunkt sehen wir bei
-
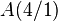
- Lösung des Gleichungssystems
-
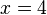und 
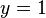
Einsetzungsverfahren
Im Gegensatz zur grafischen Lösung versuchen wir hier rein mathematisch durch Berechnung auf das Ergebnis zu kommen.
Das Ziel dabei ist es, die beiden Gleichungen auf eine Gleichung zu reduzieren, in welche nur noch eine Unbekannte steht. Hierfür lösen wir eine der beiden Gleichungen nach einer (geeigneten) Unbekannten um. Im Beispiel stellen wir die erste Gleichung nach 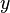um:
Da wir nun wissen, dass 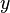identisch ist zu 
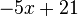können wir eben dieses 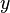in der zweiten Gleichung ersetzen und erhalten damit die Gleichung 
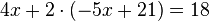. Nicht vergessen dürfen wir hier die Klammern!
Wir haben durch Umformen und Einsetzen also eine Gleichung erhalten, in der wir nur noch eine Unbekannte haben. Diese können wir dann durch Äquivalenzumformungen lösen: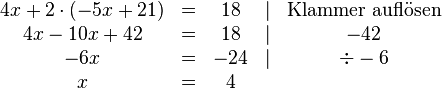
Wir haben somit den Wert für gefunden.
Um den noch fehlenden Wert für 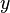berechnen zu können nehmen wir die oben umgestellte Gleichung 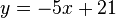und setzen den eben erhaltenen Wert von ein: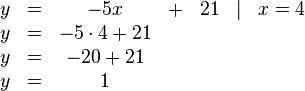
Somit haben wir auch über dieses Verfahren die Werte für und 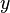gefunden.
Zusammenfassung
- Eine der Gleichungen umformen
-
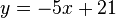
- Das Ergebnis in die zweite Gleichung einsetzen
-
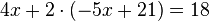
- Auflösen liefert Ergebnis für die erste Unbekannte
-
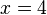
- In die zuerst umgeformte Gleichung einsetzen
-
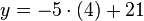
- Auflösen liefert Ergebnis für die zweite Unbekannte
-
