Kongruenz: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Einführung == In dem (zugegebenermaßen schon äteren) Film [https://www.youtube.com/watch?v=QpMVMS3F4mQ] wird gezeigt, wie Fingerabdrücke miteinander ver…“) |
(kein Unterschied)
|
Version vom 26. September 2016, 11:19 Uhr
Inhaltsverzeichnis
Einführung
In dem (zugegebenermaßen schon äteren) Film [1] wird gezeigt, wie Fingerabdrücke miteinander verglichen werden.
Man vergleicht dabei Formen von einem unbekannten Fingerabdruck mit denen eines bekannten Fingerabdrucks.
Genau nach diesem Schema werden wir für einfachere Formen auch vorgehen.
Kongruenz
Wir nennen zwei Formen kongruent, wenn diese denkungsgleich sind (wie z.B. bei den Fingerabdrücken). Die Figuren können dabei auch gedreht oder gespiegelt sein.
Beispiele
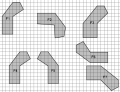
Im Bild rechts sind folgende Figuren zueinander kongruent:
- F1, F4, F6 und da man die Form auch spiegeln kann auch F5
- F3 und F7
- F2 ist zu keiner anderen Form kongruent
Feststellen der Kongruenz
Die Kongruenz zwischen Figuren können wir auf 3 Arten bestimmen:
- Wir schneiden die Formen aus und überprüfen, welche sich exakt übereinander legen lassen.
- Wir malen die Umrisse der Formen auf Transparentfolie ab und überprüfen damit die anderen Formen.
- Wir überprüfen alle Winkel und Seiten, ob diese gleich groß und in der gleichen Reihenfolge in den Formen existieren.
Die ersten beiden Möglichkeiten sind im Normalfall recht aufwändig und ungenau. Wir werden uns deshalb die dritte Möglichkeit näher anschauen.
Seiten und Winkel überprüfen
Wenn wir sämtliche Seitenlängen und Winkel der nebenstehenden Figuren messen und vergleichen, so stellen wir fest, dass diese in allen 3 Formen übereinstimmen. Lediglich die ist bei Figur 3 die Reihenfolge "gedreht" und somit die Form gespiegelt.
Formal müssen wir also bei einem Winkel beginnen und dann reihum um die Form wandern und dabei unsere Werte notieren. Z.B. ergibt sich dabei für die Form 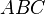 wenn wir beim Winkel
wenn wir beim Winkel 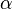 beginnen (W bedeutet dabei einen Winkel, S eine Seitenlänge)
beginnen (W bedeutet dabei einen Winkel, S eine Seitenlänge)
- W(63,43) - S(4) - W(33,69) - S(3,61) - W(82,87) - S(2,24)
Um die anderen Formen zu überprüfen suchen wir darin ebenfalls wieder den ersten Winkel von 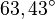 und kontrollieren dann, ob wir obige Reihenfolge in dieser Form wiederfinden. Dabei spielt es keine Rolle, in welche Richtung wir von dem Anfangswinkel ausgehen!
und kontrollieren dann, ob wir obige Reihenfolge in dieser Form wiederfinden. Dabei spielt es keine Rolle, in welche Richtung wir von dem Anfangswinkel ausgehen!
Konstruktion von kongruenten Formen
Ähnlich verhält es sich bei der Konstruktion von kongruenten Formen.
Hierzu stellen wir zunächst wieder eine Reihenfolge der ursprünglichen Form auf (wir beginnen bei 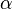 ):
):
- W(90) - S(3) - W(153.43) - S(4.47) - W(34.7) - S(7.07) - W(81.87) - S(3)
Im nächsten Schritt suchen wir bereits vorhandene Übereinstimmungen im Anfang der neuen Form. Hier finden wir die Übereinstimmung W(90) - S(3). Diese Übereinstimmung finden wir, ausgehend vom Winkel  sowohl im Uhrzeigersinn, als auch gegen den Uhrzeigersinn. Es gibt also mehrere Lösungen um die kongruente Form zu konstruieren.
sowohl im Uhrzeigersinn, als auch gegen den Uhrzeigersinn. Es gibt also mehrere Lösungen um die kongruente Form zu konstruieren.
Bei der ersten Möglichkeit zeichnen wir den nächsten Winkel von 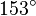 am Punkt F. und von dort eine Strecke von
am Punkt F. und von dort eine Strecke von 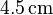 . Bei der zweiten Möglichkeit zeichnen wir den Winkel von
. Bei der zweiten Möglichkeit zeichnen wir den Winkel von 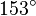 am Punkt G.
am Punkt G.


 kongruente Form gebildet werden.
kongruente Form gebildet werden.

