Gleichförmige Bewegung

Vorwissen

keines

Versuch 1

Aufbau und Durchführung

Wir benutzen eine Luftkissenbahn mit einem daraufgesetzten Wagen und stoßen diesen an, so dass er mit geringer Geschwindigkeit fährt.

Beobachtung ohne Messung

Rein aus der Betrachtung des fahrenden Wagens können wir schon erahnen, dass dieser gleichmäßig mit konstanter Geschwindigkeit fährt. Um dies zu überprüfen führen wir eine Messung durch, indem wir die pro Sekunde zurückgelegte Strecke am angelegten Maßstab ablesen.

Messung

Als Zeitgeber benutzen wir ein Metronom, welches im Sekundentakt tickt. So können wir am Maßband bei jedem Tick die Strecke ablesen und daraus berechnen, wie weit der Wagen in der letzten Sekunde gefahren ist.

Ergebnisse

An den Messwerten sehen wir -- je nach Ablesegenauigkeit -- dass sich der Wagen tatsächlich mit konstanter Geschwindkeit bewegt. Da wir allerdings mit dieser einfachen Messung die Strecke nur recht ungenau ablesen können, erhalten wir hier unter Umständen auch stärkere Schwankungen. Für ein genaueres Messergebnis müssten wir ein genaueres Messverfahren benutzen.

Definition

Wir sprechen von einer gleichförmigen Bewegung, wenn sich ein Körper mit gleichbleibender, d.h. konstanter Geschwindigkeit bewegt.

Formeln

Wir wissen aus dem Alltag: wenn wir mit einer konstanten Geschwindigkeit z.B. mit dem Fahrrad eine bestimmte Zeit lang fahren, so haben wir mit dieser Geschwindigkeit 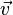un der Zeit 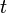die Strecke 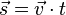zurückgelegt.

Diese Beziehung können wir natürlich durch Äquivalenzumformungen umstellen:

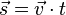
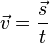
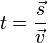
Als mathematische Symbole verwenden wir: 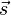für die Strecke, 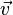für velocity (englisch für Geschwindigkeit) und 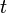für time (engl. Zeit).

(Vektor-) Pfeile über den Symbolen

Über einigen der Symbolen stehen sogenannte Vektorpfeile. Diese geben an, dass wir uns (zumindest bei späteren Betrachtungen) nicht nur für die Größe des Wertes interessieren sondern auch für dessen Richtung. Vorerst können wir bei der Benutzung der Formel zur Berechnung der fehlenden Werten jedoch diese Pfeile ignorieren.

Diagrammdarstellungen

Die gleichförmige Bewegung können wir auch in Diagrammen darstellen. Zum einen können wir die zurückgelegte Strecke über der Zeit, d.h. ein 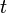--Diagrann, aufzeichnen. Wir erkennen hierbei, dass die Strecke proportional mit der Zeit wächst. Je schneller der Wagen fährt, desto steiler ist dabei die Gerade.

Im 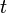--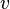Diagramm sehen wir hingegen, dass die Geschwindigkeit immer konstant, d.h. unabhängig von der Zeit immer auf der selben Höhe bleibt.