Lineare Gleichungen: Unterschied zwischen den Versionen
(→Beispiel) |
(→Beispiel) |
||
| Zeile 96: | Zeile 96: | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | x+5&=&11&\qquad|\ -5\\ | + | &x+5&=&11&\qquad|\ -5\\ |
| − | \iff\quad (x+5)-5&=&(11)-5&\qquad|\ \text{Klammern auflösen}\\ | + | \iff\quad &(x+5)-5&=&(11)-5&\qquad|\ \text{Klammern auflösen}\\ |
| − | \iff\quad x+5-5&=&11-5&\qquad|\ \text{zusammenfassen}\\ | + | \iff\quad &x+5-5&=&11-5&\qquad|\ \text{zusammenfassen}\\ |
| − | \iff\quad x&=&6 | + | \iff\quad &x&=&6 |
\end{matrix}</math> | \end{matrix}</math> | ||
Version vom 8. Juni 2015, 10:21 Uhr
Inhaltsverzeichnis
Vorwissen
Gleichungen
Viele Probleme des Alltags können mathematisch in einer Gleichung beschrieben und gelöst werden. Die wohl bekannteste Gleichung ist von Einstein: 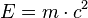 .
.
Gleichungen geben eine Beziehung zwischen zwei Termen an, und zwar dahingehend, dass die Terme auf beiden Seiten des Gleichzeichens den gleichen Wert annehmen.
Grundproblem
Gleichungen können wir dazu benutzen, um Lösungen für unbekannte Werte zu bestimmen. Als einfaches Beispiel betrachten wir die Gleichung
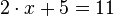
Welchen Wert müssen wir für  einsetzen, damit die Gleichung stimmt?
einsetzen, damit die Gleichung stimmt?
Einfaches Beispiel mit Wertetabelle
Den richtigen Wert für  können durch ausprobieren herausfinden. Hierfür verwenden wir für den Term auf der linken Seite eine Wertetabelle:
können durch ausprobieren herausfinden. Hierfür verwenden wir für den Term auf der linken Seite eine Wertetabelle:
 |
linke Seite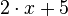 |
rechte Seite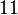
|
|---|---|---|
| 0 | 5 | 11 |
| 1 | 7 | 11 |
| 2 | 9 | 11 |
| 3 | 11 | 11 |
| 4 | 13 | 11 |
| 5 | 15 | 11 |
| 6 | 17 | 11 |
Wie wir jetzt in der Tabelle ablesen können, stimmen der Term 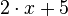 (linke Seite) und der Term
(linke Seite) und der Term 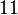 (rechte Seite) gerade dann überein, wenn wir für
(rechte Seite) gerade dann überein, wenn wir für  den Wert
den Wert 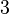 einsetzen. Die Lösungsmenge der Gleichung ist also
einsetzen. Die Lösungsmenge der Gleichung ist also
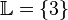
komplexeres Beispiel mit Wertetabelle
Auch Lösungen für komplexere Gleichungen, in denen die Variable auf beiden Seiten vorkommt, können wir mit einer Wertetabelle lösen. Betrachten wir hierfür die Gleichung
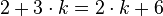
Wir stellen wieder die Wertetabelle auf:
 |
linke Seite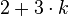 |
rechte Seite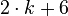
|
|---|---|---|
| 0 | 2 | 6 |
| 1 | 5 | 8 |
| 2 | 8 | 10 |
| 3 | 11 | 12 |
| 4 | 14 | 14 |
| 5 | 17 | 16 |
| 6 | 20 | 18 |
Die Gleichheit beider Seiten ist also gerade dann erfüllt, wenn wir für 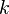 den Wert
den Wert 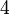 einsetzen, Die Lösungsmenge ist also:
einsetzen, Die Lösungsmenge ist also:
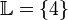
Äquivalenzumformungen
Das Lösen von Gleichungen mithilfe einer Wertetabelle funktioniert nur dann gut, wenn die Lösung ganzzahlig und recht klein ist. Anderenfalls ist dieser Lösungsweg sehr aufwändig. Besser wäre es, wenn wir die Lösung einer Gleichung direkt berechnen könnten.
Das Waagemodell
Wir können uns eine Gleichung als Balkenwaage vorstellen. Damit diese ausgeglichen ist, müssen die Gegenstände auf beiden Seiten gleich schwer sein. Verändern wir etwas auf einer Seite, so müssen wir dieselbe Änderung auch auf der anderen Seite durchführen damit die Waage im Gleichgewicht bleibt.
Wir können beispielsweise auf beiden Seiten jeweils 1kg mehr dazu legen oder wegnehmen, dann bleibt die Waage trotzdem im Gleichgewicht.
Genauso können wir auch mit einer Gleichung verfahren: da wir wissen, dass die Terme auf beiden Seiten gleich sind bzw. das Gleiche beinhalten ist unsere "Gleichungswaage" ausgeglichen. Wir können jetzt auf beiden Seiten jeweils einen Wert hinzufügen (addieren) oder wegnehmen (subtrahieren) so dass die neue Gleichung äquivalent zur alten ist.
Äquivalent kommt aus dem lateinischen und setzt sich aus den Teilwörtern aequus (gleich) und valens (wertig) zusammen, und bedeutet also gleichwertig. Gleichwertige Gleichungen sind solche, die die selbe Lösungsmenge besitzen.
Addieren oder subtrahieren wir auf beiden Seiten den selben Wert, so ändert sich die Lösungsmenge nicht, die beiden Gleichungen sind also äquivalent. Man nennt so eine Umformung deshalb auch Äquivalenzumformung.
Beispiel
Wir betrachten die Gleichung:
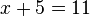
Subtrahieren wir auf beiden Seiten jeweils den Wert 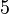 so bekommen wir:
so bekommen wir:
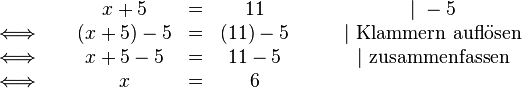
Die Lösungsmenge der Gleichung ist also
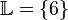
formelles
Um darzustellen, welche Umformung man zum nächsten Schritt durchführt gibt man hinter der Gleichung die jeweilige Aktion an. Vor die umgeformte Gleichung schreiben wir einen Aquivalenzpfeil 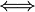 um anzugeben, dass diese beiden Gleichungen äquivalent sind.
um anzugeben, dass diese beiden Gleichungen äquivalent sind.