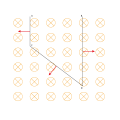Kraft auf stromdurchflossenen Leiter: Unterschied zwischen den Versionen
(→Aufgabe 2) |
|||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
Betrachten wir unseren stromdurchflossenen Leiter, so wissen wir, dass sich darin die Elektronen mit einer Ladung von <math>q=e^-=1.602\cdot10^{-19}\,\mathrm{C}</math> bewegen. Jedoch können wir die Geschwindigkeit noch nicht direkt angeben. | Betrachten wir unseren stromdurchflossenen Leiter, so wissen wir, dass sich darin die Elektronen mit einer Ladung von <math>q=e^-=1.602\cdot10^{-19}\,\mathrm{C}</math> bewegen. Jedoch können wir die Geschwindigkeit noch nicht direkt angeben. | ||
| − | Nach der Definition der [[ | + | Nach der Definition der [[elektrischer Strom#Die_elektrische_Stromstärke|elektrischen Stromstärke]] <math>I</math> gibt diese an, welche Ladungsmenge in einer bestimmten Zeit durch einen Leiter fließt. Es gilt also: |
<math>I=\frac qt\iff q=I\cdot t</math> | <math>I=\frac qt\iff q=I\cdot t</math> | ||
| Zeile 53: | Zeile 53: | ||
== Aufgabe 2 == | == Aufgabe 2 == | ||
| − | In einem Magnetfeld befindet sich ein <math>l=10\,\mathrm{cm}</math> langer elektrischer Leiter. Auf diesen wirkt eine Kraft von <math>F=1.0\,\mathrm{mN}</math>. Die elektrische Stromstärke beträgt < | + | In einem Magnetfeld befindet sich ein <math>l=10\,\mathrm{cm}</math> langer elektrischer Leiter. Auf diesen wirkt eine Kraft von <math>F=1.0\,\mathrm{mN}</math>. Die elektrische Stromstärke beträgt <math>I=3.0\,\mathrm A</math>. |
# Wie groß ist die magnetische Flussdichte <math>B</math>, wenn der Leiter senkrecht zu den magnetischen Feldlinien steht? | # Wie groß ist die magnetische Flussdichte <math>B</math>, wenn der Leiter senkrecht zu den magnetischen Feldlinien steht? | ||
Aktuelle Version vom 31. März 2016, 18:44 Uhr
Inhaltsverzeichnis
Vorwissen
Versuch
Versuchsaufbau+Durchführung: Wir hängen einen Leiter in ein Magnetfeld (z.B. Hufeisenmagnet) und lassen einen Strom durch den Leiter fließen.
Beobachtung: Der Leiter wird - je nach Stromrichtung - entweder aus dem Magnet herausgedrückt, oder in den Magnet hineingezogen.
Erklärung: Wir können das Phänomen mit der Lorentzkraft beschreiben.
Kraft auf stromdurchflossenen Leiter
Wir wollen nun wissen, welche Kraft auf den Leiter wirkt. Dazu gehen wir von der Lorentzkraft aus:
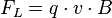
Wobei 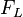 die Lorentzkraft,
die Lorentzkraft, 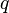 die Ladung,
die Ladung, 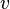 die Geschwindigkeit der Teilchen und
die Geschwindigkeit der Teilchen und 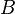 die Stärke des Magnetfeldes angibt.
die Stärke des Magnetfeldes angibt.
Betrachten wir unseren stromdurchflossenen Leiter, so wissen wir, dass sich darin die Elektronen mit einer Ladung von 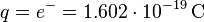 bewegen. Jedoch können wir die Geschwindigkeit noch nicht direkt angeben.
bewegen. Jedoch können wir die Geschwindigkeit noch nicht direkt angeben.
Nach der Definition der elektrischen Stromstärke 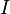 gibt diese an, welche Ladungsmenge in einer bestimmten Zeit durch einen Leiter fließt. Es gilt also:
gibt diese an, welche Ladungsmenge in einer bestimmten Zeit durch einen Leiter fließt. Es gilt also:
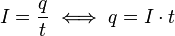
Für die Geschwindigkeit kennen wir aus der Mechanik den Zusammenhang
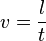
mit der Strecke bzw. der Leiterlänge 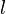 und der Zeit
und der Zeit 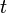 .
.
Setzen wir diese beiden Zusammenhänge in die Formel für die Lorentzkraft ein so erhalten wir:
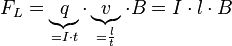
Auf einen Leiter der Länge 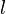 in einem Magnetfeld
in einem Magnetfeld 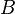 wirkt bei einer Stromstärke
wirkt bei einer Stromstärke 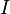 also die Kraft
also die Kraft
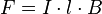
Aufgabe 1
Das magnetische Feld eines Dauermagneten in einem Drehspulinstrument besitzt die magnetische Flussdichte 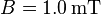 . Auf ein zu diesem Magnetfeld senkrechtes Leiterstück der Länge
. Auf ein zu diesem Magnetfeld senkrechtes Leiterstück der Länge 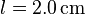 wirkt die Kraft
wirkt die Kraft 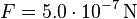 .
.
Wie groß ist die elektrische Stromstärke 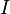 ?
?
Lösung
gegeben: 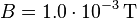 ,
, 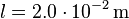 ,
, 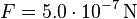
gesucht: 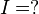
Formel umstellen: 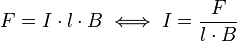
einsetzen: 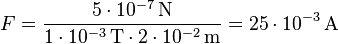
Antwort: Durch den Leiter fließt eine Stromstärke von 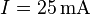
Aufgabe 2
In einem Magnetfeld befindet sich ein 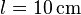 langer elektrischer Leiter. Auf diesen wirkt eine Kraft von
langer elektrischer Leiter. Auf diesen wirkt eine Kraft von 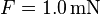 . Die elektrische Stromstärke beträgt
. Die elektrische Stromstärke beträgt 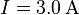 .
.
- Wie groß ist die magnetische Flussdichte
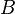 , wenn der Leiter senkrecht zu den magnetischen Feldlinien steht?
, wenn der Leiter senkrecht zu den magnetischen Feldlinien steht? - Wie groß ist die magnetische Flussdichte
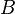 , wenn der Winkel zwischen Leiter und magnetischen Feldlinien
, wenn der Winkel zwischen Leiter und magnetischen Feldlinien 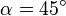 beträgt?
beträgt?
Lösung 1
gegeben: 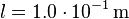 ,
, 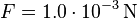 ,
, 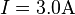
gesucht: 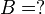
Formel umstellen: 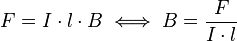
einsetzen und ausrechnen ergibt: Die magnetische Flussdichte beträgt 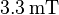
Lösung 2
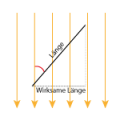
Ist der Leiter nicht senkrecht zum Magnetfeld, so müssen wir zunächst die vektorielle Geschwindigkeit zerlegen. Die Lorentzkraft wirkt nämlich nur auf den Anteil, der senkrecht zum Magnetfeld steht. Die wirksame Länge - also diejenige, die senkrecht zum Magnetfeld steht - berechnet sich aus der Länge multipliziert mit dem Sinus des Winkels:
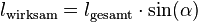
Für die Kraft auf einen schräg im Magnetfeld liegenden Leiter gilt also:
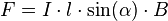
Anmerkung: natürlich gilt diese Formel immer, da bei einem senkrechten Leiter 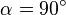 und damit
und damit 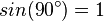 gilt.
gilt.
Zur Lösung der Aufgabe müssen wir also lediglich diese Formel verwenden:
gegeben: 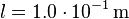 ,
, 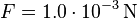 ,
, 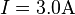 ,
, 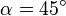
gesucht: 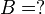
Formel umstellen: 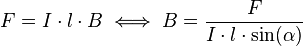
einsetzen und ausrechnen ergibt: Die magnetische Flussdichte beträgt 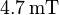
Aufgabe 3
Das abgebildete quadratische Leiterrähmchen besitzt 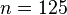 Windungen, seine Seitenlänge beträgt
Windungen, seine Seitenlänge beträgt 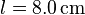 und seine Masse
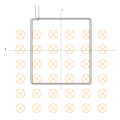
und seine Masse 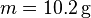 . Es befindet sich nur zum Teil in einem homogenen Magnetfeld, das senkrecht in die Bildebene hinein zeigt. Die Rahmenquerschnittsfläche wird senkrechtvom Magnetfeld durchsetzt.
. Es befindet sich nur zum Teil in einem homogenen Magnetfeld, das senkrecht in die Bildebene hinein zeigt. Die Rahmenquerschnittsfläche wird senkrechtvom Magnetfeld durchsetzt.
- Fließt durch die Leiterwindungen des Rahmens ein Gleichstrom der Stärke
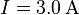 in geeigneter Richtung, dann wird seine Gewichtskraft genau kompensiert. Welches Ende des Leiters ist mit dem Plus- welches mit dem Minuspol der Spannungsquelle verbunden?
in geeigneter Richtung, dann wird seine Gewichtskraft genau kompensiert. Welches Ende des Leiters ist mit dem Plus- welches mit dem Minuspol der Spannungsquelle verbunden? - Berechne die magnetische Flussdichte
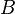
- Begründe, warum so ein Kräftegleichgewicht unmöglich ist, wenn der Rahmen vollständig in das Magnetfeld eingetaucht ist.
- Das Rähmchen ist nun drehbar um die Achse v gelagert. Bestimme, um welchen Winkel
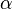 es aus der abgebildeten Stellung zu drehen ist, damit seine Gewichtskraft bei einer Stromstärke von
es aus der abgebildeten Stellung zu drehen ist, damit seine Gewichtskraft bei einer Stromstärke von 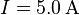 kompensiert wird.
kompensiert wird.
Lösung 1
Mithilfe der linken-Hand-Regel der Lorentzkraft können wir direkt herausfinden, dass die Kraft auf die linke Seite des Leiterrahmens der Kraft auf der rechte Seite des Leiterrahmens entgegengesetzt ist und sich somit genau aufhebt. Wir müssen also lediglich die untere Seite betrachten.
Damit die Lorentzkraft die Gewichtskraft kompensieren kann muss sie entgegen der Gewichtskraft, d.h. nach oben wirken. Mit der linken-Hand-Regel können wir damit sehr schnell bestimmen, dass an der Unterseite des Leiterrahmens die Elektronen nach links fließen müssen, so dass im Bild am vorderen Anschluss der Pluspol sein muss.
Lösung 2
Die wirksame Länge des im Magnetfeld befindlichen Leiters ist jetzt
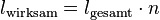
Somit gilt für die Kraft:
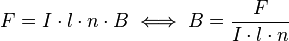
Da die Gewichtskraft kompensiert werden soll, muss diese zunächst berechnet werden:
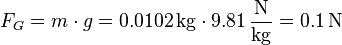
Setzt man die sonstigen gegebenen Werte in die Formel ein, so erhält man 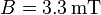
Lösung 3
Wenn der Leiterrahmen komplett im Magnetfeld wäre, so würde auf das obere Ende ebenfalls eine Kraft wirken. Diese wäre genau der Kraft auf das untere Ende des Rahmens entgegengesetzt und würde sich - ebenso wie die beiden Kräfte an linker und rechter Seite - genau aufheben.
Lösung 4
Die wirksame Leiterlänge an der Unterkante bei Drehung ist

Für die Kraft gilt also:

Einsetzen und ausrechnen ergibt einen Winkel von 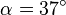
Aufgabe 4
Bei dem abgebildeten Leiter sind die vertikalen Stücke zueinander parallel. Es ist 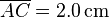 ,
, 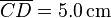 und
und 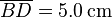 . Er wird von einem Gleichstrom
. Er wird von einem Gleichstrom 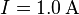 durchflossen (Elektronen von A nach B) und befindet sich vollständig in einem Magnetfeld mit
durchflossen (Elektronen von A nach B) und befindet sich vollständig in einem Magnetfeld mit 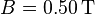 .
.
- Berechne die Kraftbeträge auf die einzelnen Leiterstücke.
- Was kann man über die resultierende Gesamtkraft aussagen?
Lösung 1
Die Kraftbeträge lassen sich direkt mit der Formel 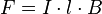 berechnen:
berechnen:
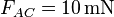
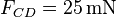
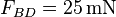
Lösung 2
Anstatt den Abschnitt 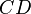 direkt zu bestimmen können wir diesen auch wieder zerlegen in eine horizontale und eine vertikale Richtung. Der vertikale Abstand ist
direkt zu bestimmen können wir diesen auch wieder zerlegen in eine horizontale und eine vertikale Richtung. Der vertikale Abstand ist 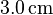 , da hiermit ja der Unterschied zwischen der Länge
, da hiermit ja der Unterschied zwischen der Länge 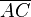 und
und 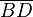 ausgeglichen wird. Der horizontale Abstand ergibt sich dann nach dem Pythagoras mit
ausgeglichen wird. Der horizontale Abstand ergibt sich dann nach dem Pythagoras mit 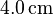 .
.
Betrachten wir diese Richtungen separat, so können wir auch die Kräfte separat bestimmen (die Gesamtkraft bleibt dabei jedoch gleich!).
Für die vertikale Stromrichtung ergibt sich damit eine Kraft von 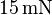 nach links, für die horizontale Stromrichtung eine Kraft von
nach links, für die horizontale Stromrichtung eine Kraft von 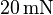 .
.
Betrachten wir den Gesamten Leiter, so erkennen wir, dass die Kräfte welche nach links wirken und die Kräfte die nach rechts wirken aufsummiert gleich gro sind und sich somit gerade aufheben. Somit bleibt als Gesamtkraft lediglich die Kraft übrig, die aus der horizontalen Stromrichtung, also aus dem horizontalen Abstand folgt.