Abstand Punkt-Gerade: Unterschied zwischen den Versionen
(→formell) |
(→formell) |
||
| Zeile 42: | Zeile 42: | ||
=== formell === | === formell === | ||
| − | Diese Folgerung kann auch mathematisch mit dem Skalarprodukt bewiesen werden. | + | Diese Folgerung kann auch mathematisch mit dem Skalarprodukt bewiesen werden: |
| + | |||
| + | <math>|\vec{RP}|\text{ minimal}\iff\vec{RP}\perp\vec u</math> | ||
| + | |||
| + | Hier soll jedoch nur die <math>\Leftarrow</math>-Richtung gezeigt werden, welches der Behauptung entspricht: '''ist <math>\vec{RP}</math> orthogonal zu <math>\vec u</math>, dann ist <math>|\vec{RP}|</math> minimal.''' | ||
Version vom 19. Mai 2015, 19:43 Uhr
Inhaltsverzeichnis
[Verbergen]Vorwissen
Vektoren, Skalarprodukt, Geraden im Raum, Ebenen im Raum, Normalenvektor, Schnittpunkt Gerade-Ebene
Problem
Wir haben eine Gerade 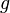 im Raum und einen Punkt
im Raum und einen Punkt 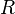 welcher nicht auf der Geraden liegt. Wir können bisher noch keinen Abstand zwischen Punkt und Gerade berechnen.
welcher nicht auf der Geraden liegt. Wir können bisher noch keinen Abstand zwischen Punkt und Gerade berechnen.
Beispielsweise spielt der Abstand bei Planung eines Flughafens eine Rolle, denn hier können die Bahnen der startenden und landenden Flugzeuge als Gerade angenähert werden. Dabei muss immer ein gewisser minimaler Sicherheitsabstand zu umliegenden Gebäuden eingehalten werden.
Erinnerung
In einer früheren Klasse wurde das Problem bereits im zweidimensionalen behandelt. Hier wurde der Abstand gemessen indem das Geodreieck orthogonal so auf die Gerade gelegt wurde dass der Punkt auf der Skala liegt. Dann konnte der Abstand rechtwinklig am Geodreieck abgelesen werden.
Animation
Um das Problem eines startenden Flugzeugs zu verdeutlichen gibt es folgende Animation. Das Flugzeug kann dabei an der unteren Ecke entlang der Geraden verschoben werden:
Aufgrund der Problemstellung, dass ein minimaler Sicherheitsabstand eingehalten werden muss ergibt sich folgende Definition.
Definition
Als Abstand zwischen einer Geraden 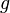 und einem Punkt
und einem Punkt 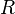 ist definiert als kleinstmöglicher Abstand zwischen diesen beiden.
ist definiert als kleinstmöglicher Abstand zwischen diesen beiden.
formell
Eine Gerade ist definiert als Punktmenge (mit 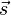 : Stützvektor und
: Stützvektor und 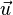 : Richtungsvektor, vgl. Geraden im Raum):
: Richtungsvektor, vgl. Geraden im Raum):
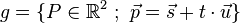
dann gilt für den Abstand
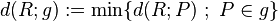
Folgerung
Wie wir in der Animation auch anschaulich erkennen können, ist dieser minimale Abstand gerade dann gegeben, wenn der Verbindungsvektor 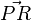 orthogonal zur Geraden, bzw. deren Richtungsvektor
orthogonal zur Geraden, bzw. deren Richtungsvektor 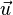 steht, d.h. das Skalarprodukt Null ergibt.
steht, d.h. das Skalarprodukt Null ergibt.
formell
Diese Folgerung kann auch mathematisch mit dem Skalarprodukt bewiesen werden:
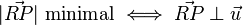
Hier soll jedoch nur die 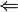 -Richtung gezeigt werden, welches der Behauptung entspricht: ist
-Richtung gezeigt werden, welches der Behauptung entspricht: ist 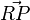 orthogonal zu
orthogonal zu 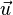 , dann ist
, dann ist 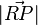 minimal.
minimal.