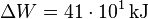Spezifische Wärmekapazität: Unterschied zwischen den Versionen
K (Akimmig verschob die Seite INF Diskussion:Spezifische Wärmekapazität nach PH:Spezifische Wärmekapazität, ohne dabei eine Weiterleitung anzulegen) |
|||
| Zeile 101: | Zeile 101: | ||
''Lösung:'' Da die Sonneneinstrahlung weltweit in etwa gleich ist (bezogen auf den Einstrahlwinkel, s. [[PH:Solarkonstante|Solarkonstante]]) liefert die Sonne im Meer und in der Wüste die gleiche Energiemenge. Da allerdings die spezifische Wärmekapazität für Sand deutlich niedriger ist bedeutet das, dass bei gleicher zugeführter Energiemenge die Temperatur des Sandes stärker zunimmt als die des Wassers. | ''Lösung:'' Da die Sonneneinstrahlung weltweit in etwa gleich ist (bezogen auf den Einstrahlwinkel, s. [[PH:Solarkonstante|Solarkonstante]]) liefert die Sonne im Meer und in der Wüste die gleiche Energiemenge. Da allerdings die spezifische Wärmekapazität für Sand deutlich niedriger ist bedeutet das, dass bei gleicher zugeführter Energiemenge die Temperatur des Sandes stärker zunimmt als die des Wassers. | ||
| + | |||
| + | === Tee kochen === | ||
| + | Wie viel Energie wird benötigt, um <math>1.5\,\mathrm{l}</math> Wasser zu kochen? Dabei nehmen wir an, dass das Wasser mit einer Temperatur von <math>23^\circ\,\mathrm{C}</math> aus dem Wasserhahn kommt und bei ca. <math>98^\circ\,\mathrm{C}</math> kocht. (Etwa <math>600\,\mathrm{m}</math> über NN) | ||
| + | |||
| + | ''Lösung:'' Für Wasser gilt: <math>c=4.18\frac{\mathrm{kJ}}{\mathrm{kg}\,\mathrm{K}}</math>, als Masse nehmen wir <math>m=1.5\,\mathrm{kg}</math> (die Dichte nehmen wir hier mit <math>1\frac{\mathrm{kg}}{\mathrm{l}}</math> an). Als Temperaturdifferenz haben wir: <math>\Delta\theta=98-23\,\mathrm{K}=65\,\mathrm{K}</math>. | ||
| + | |||
| + | Somit gilt: <math>\Delta W=c\cdot\Delata\theta\cdot m=4.18\cdot65\cdot1.5\,\mathrm{kJ}=407.55\,\mathrm{kJ}</math> Mit der [[PH:Ziffernregel|Ziffernregel]] erhalten wir <math>\Delta W=41\cdot10^1\,\mathrm{kJ}</math> | ||
Version vom 30. April 2015, 08:10 Uhr
Inhaltsverzeichnis
[Verbergen]Vorwissen
Grundfrage
Wenn ich einen Topf mit Wasser habe, wie viel kostet es mich, dieses Wasser zum Kochen zu bringen?
Hierzu müssen wir wissen:
- Die Energiekosten
- Diese liegen derzeit im Deutschlandschnitt bei knapp 30ct pro kWh
- Den Energieverbrauch des Tauchsieders/Kochplatte/...
- Hierfür können wir entweder direkt ein Energiemessgerät benutzen
- oder diese aus der Leistung des Tauchsieders berechnen, denn es gilt
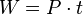
Vermutungen
Von welchen Eigenschaften bzw. Größen hängt die Energiemenge ab?
- Masse des Wassers
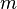
- Ausgangstemperatur bzw. der Temperaturdifferenz
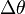 die wir erreichen wollen
die wir erreichen wollen - Stoffart (Wasser, Öl, aber auch Feststoffe wie z.B. Glas, Kupfer, Blei,...)
Vorüberlegungen
Wie können wir denn den Zusammenhang dieser Größen messen? Welche Informationen brauchen wir dazu?
- Zur Temperaturdifferenz
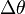 brauchen wir die Anfangstemperatur
brauchen wir die Anfangstemperatur 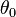 , denn es gilt:
, denn es gilt: 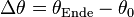
- Die zugeführte Wärmemenge
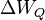 , die in einer Änderung der inneren Energie resultiert können wir bestimmen über die abgegebene Energie des Tauchsieders. Wir nehmen dazu (idealisiert) an, dass die gesamte abgegebene Energiemenge als innere Energie in das Wasser übergeht.
, die in einer Änderung der inneren Energie resultiert können wir bestimmen über die abgegebene Energie des Tauchsieders. Wir nehmen dazu (idealisiert) an, dass die gesamte abgegebene Energiemenge als innere Energie in das Wasser übergeht. - Die Masse
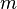 des Wassers.
des Wassers.
Versuche
Zusammenhang zwischen 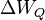 und
und 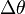
In diesem Versuch wollen wir überprüfen, wie die zugeführte Energiemenge 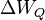 die Temperatur von Wasser verändert. Dazu verwenden wir einen Tauchsieder um eine bestimmte Menge an Wasser zu erwärmen.
die Temperatur von Wasser verändert. Dazu verwenden wir einen Tauchsieder um eine bestimmte Menge an Wasser zu erwärmen.
Wir führen dazu einer festen Wassermenge unterschiedliche Energiemengen zu indem wir den Tauchsieder unterschiedlich lange im Wasser lassen bzw, die Temperatur nach unterschiedlichen Zeiten messen.
Ergebnis: 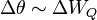
Zusammenhang zwischen 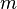 und
und 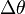
Wir überprüfen, wie stark sich die Temperatur des Wassers ändert, wenn man eine feste Energiemenge aber unterschiedliche Wassermassen betrachtet.
Wir führen dazu nacheinander unterschiedlichen Wassermassen jeweils eine feste Energiemenge zu und messen die Erhöhung der Temperatur.
Ergebnis: 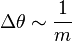
Zusammenhang zwischen 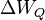 und
und 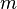
Abschließend überprüfen wir noch, welche Energiemenge benötigt wird um unterschiedliche Wassermassen um eine feste Temperaturdifferenz zu erreichen.
Dazu nehmen wir wieder unterschiedliche Wassermassen und erwärmen so lange, bis wir die gewünschte Temperaturdifferenz erreichen.
Ergebnis: 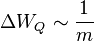
Ergebnis der Versuche
Für Proportionalitäten gilt immer: wenn 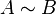 und
und 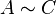 dann gilt auch
dann gilt auch 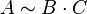
Setzen wir diese Ergebnisse zusammen, so erhalten wir 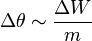
Jede Proportionalität können wir mit einer Proportionalitätskonstanten auch als Gleichung schreiben: 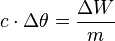
Durch Umformung erhalten wir die spezifische Wärmekapazität 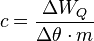 mit
mit 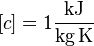
Die spezifische Wärmekapazität gibt also an, wie viel Energie man einem Körper der Masse 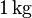 zuführen muss um bei deisem eine Temperaturerhöhung von
zuführen muss um bei deisem eine Temperaturerhöhung von 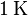 zu erreichen
zu erreichen
Für Wasser gilt: 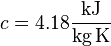
unterschiedliche Materialien
Bisher haben wir lediglich Wasser betrachtet. Wir wollen jetzt noch unterschiedliche Materialien (auch Feststoffe) untersuchen. Hierfür haben wir kleine Blei- und Glaskügelchen. Da wir diese nicht direkt wie bisher mit dem Tauchsieder erwärmen können werfen wir diese Kugeln in Wasser und erwärmen das "Gemisch". Hier dient das Wasser lediglich als Wärmeleiter um die Wärme auch in die Kügelchen zu leiten.
Hierbei müssen wir aber beachten, dass dann das Blei bzw. Glas die Wärme aufnimmt, aber natürlich ebenso das Wasser! Es gilt also 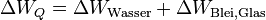 (
(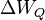 gibt die vom Tauchsieder abgegebene Energiemenge an)
gibt die vom Tauchsieder abgegebene Energiemenge an)
Um diesen Fehler also herauszurechnen nutzen wir immer die gleiche Menge an Wasser und erwärmen parallel dazu dieselbe Menge Wasser nochmals ohne Blei bzw. Glas. Durch diese Parallelmessung bekommen wir 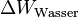 welches wir anschließend nutzen können um den Wert
welches wir anschließend nutzen können um den Wert 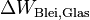 zu berechnen.
zu berechnen.
Aus diesem 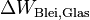 können wir dann wiederum zusammen mit der gemessenen Temperaturdifferenz und der Masse die spezifische Wärmekapazität berechnen.
können wir dann wiederum zusammen mit der gemessenen Temperaturdifferenz und der Masse die spezifische Wärmekapazität berechnen.
einige Literaturwerte
| Stoff | spezifische Wärmekapazität in 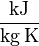
|
|---|---|
| Wasser | 4.18 |
| Glas | 0.6 bis 0.8 |
| Plexiglas | 1.47 |
| Blei | 0.13 |
| Kupfer | 0.38 |
| Sand | 0.84 |
mehr davon unter [1]
Fragen und Aufgaben
Warum ist es in der Wüste so heiß?
Mit den oben angegebenen Werten kann man auch die Frage beantworten, warum es in der Wüste, im Vergleich zum Meer, so heiß ist.
Lösung: Da die Sonneneinstrahlung weltweit in etwa gleich ist (bezogen auf den Einstrahlwinkel, s. Solarkonstante) liefert die Sonne im Meer und in der Wüste die gleiche Energiemenge. Da allerdings die spezifische Wärmekapazität für Sand deutlich niedriger ist bedeutet das, dass bei gleicher zugeführter Energiemenge die Temperatur des Sandes stärker zunimmt als die des Wassers.
Tee kochen
Wie viel Energie wird benötigt, um 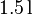 Wasser zu kochen? Dabei nehmen wir an, dass das Wasser mit einer Temperatur von
Wasser zu kochen? Dabei nehmen wir an, dass das Wasser mit einer Temperatur von 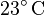 aus dem Wasserhahn kommt und bei ca.
aus dem Wasserhahn kommt und bei ca. 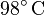 kocht. (Etwa
kocht. (Etwa 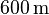 über NN)
über NN)
Lösung: Für Wasser gilt: 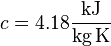 , als Masse nehmen wir
, als Masse nehmen wir 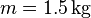 (die Dichte nehmen wir hier mit
(die Dichte nehmen wir hier mit 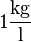 an). Als Temperaturdifferenz haben wir:
an). Als Temperaturdifferenz haben wir: 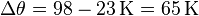 .
.
Somit gilt: Fehler beim Parsen (Unbekannte Funktion „\Delata“):
Mit der Ziffernregel erhalten wir