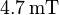Kraft auf stromdurchflossenen Leiter: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Vorwissen == Lorentzkraft == Versuch == '''Versuchsaufbau+Durchführung:''' Wir hängen einen Leiter in ein Magnetfeld (z.B. Hufeisenmagnet) und lassen…“) |
|||
| Zeile 51: | Zeile 51: | ||
Antwort: Durch den Leiter fließt eine Stromstärke von <math>I=25\,\mathrm{mA}</math> | Antwort: Durch den Leiter fließt eine Stromstärke von <math>I=25\,\mathrm{mA}</math> | ||
| + | |||
| + | == Aufgabe 2 == | ||
| + | In einem Magnetfeld befindet sich ein <math>l=10\,\mathrm{cm}</math> langer elektrischer Leiter. Auf diesen wirkt eine Kraft von <math>F=1.0\,\mathrm{mN}</math>. Die elektrische Stromstärke beträgt <ath>I=3.0\,\mathrm A</math>. | ||
| + | |||
| + | # Wie groß ist die magnetische Flussdichte <math>B>, wenn der Leiter senkrecht zu den magnetischen Feldlinien steht? | ||
| + | # Wie groß ist die magnetische Flussdichte <math>B>, wenn der Winkel zwischen Leiter und magnetischen Feldlinien <math>\alpha=45^\circ</math> beträgt? | ||
| + | |||
| + | === Lösung 1 === | ||
| + | gegeben: <math>l=1.0\cdot10^{-1}\,\mathrm{m}</math>, <math>F=1.0\cdot10^{-3}\,\mathrm{N}</math>, <math>I=3.0\mathrm A</math> | ||
| + | |||
| + | gesucht: <math>B=?</math> | ||
| + | |||
| + | Formel umstellen: <math>F=I\cdot l\cdot B\iff B=\frac F{I\cdot l}</math> | ||
| + | |||
| + | einsetzen und ausrechnen ergibt: Die magnetische Flussdichte beträgt <math>3.3\,\mathrm{mT}</math> | ||
| + | |||
| + | === Lösung 2 === | ||
| + | <gallery perrow="2" style="float:right;clear:both;"> | ||
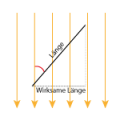
| + | Zerlegung_Laenge_im_B-Feld.png|Zerlegung der Länge im Magnetfeld | ||
| + | </gallery> | ||
| + | Ist der Leiter '''nicht senkrecht''' zum Magnetfeld, so müssen wir zunächst die vektorielle Geschwindigkeit zerlegen. Die Lorentzkraft wirkt nämlich nur auf den Anteil, der senkrecht zum Magnetfeld steht. Die wirksame Länge - also diejenige, die senkrecht zum Magnetfeld steht - berechnet sich aus der Länge multipliziert mit dem Sinus des Winkels: | ||
| + | |||
| + | <math>l_\mathrm{wirksam}=l_\mathrm{gesamt}\cdot\sin(\alpha)</math> | ||
| + | |||
| + | Für die Kraft auf einen schräg im Magnetfeld liegenden Leiter gilt also: | ||
| + | |||
| + | <math>F=I\cdot l\cdot\sin(\alpha)\cdot B</math> | ||
| + | |||
| + | ''Anmerkung: natürlich gilt diese Formel immer, da bei einem senkrechten Leiter <math>\alpha=90^\circ</math> und damit <math>sin(90^\circ)=1</math> gilt.'' | ||
| + | |||
| + | Zur Lösung der Aufgabe müssen wir also lediglich diese Formel verwenden: | ||
| + | |||
| + | gegeben: <math>l=1.0\cdot10^{-1}\,\mathrm{m}</math>, <math>F=1.0\cdot10^{-3}\,\mathrm{N}</math>, <math>I=3.0\mathrm A</math>, <math>\alpha=45^\circ</math> | ||
| + | |||
| + | gesucht: <math>B=?</math> | ||
| + | |||
| + | Formel umstellen: <math>F=I\cdot l\cdot B\iff B=\frac F{I\cdot l\cdot\sin(\alpha)}</math> | ||
| + | |||
| + | einsetzen und ausrechnen ergibt: Die magnetische Flussdichte beträgt <math>4.7\,\mathrm{mT}</math> | ||
Version vom 31. März 2016, 17:08 Uhr
Inhaltsverzeichnis
Vorwissen
Versuch
Versuchsaufbau+Durchführung: Wir hängen einen Leiter in ein Magnetfeld (z.B. Hufeisenmagnet) und lassen einen Strom durch den Leiter fließen.
Beobachtung: Der Leiter wird - je nach Stromrichtung - entweder aus dem Magnet herausgedrückt, oder in den Magnet hineingezogen.
Erklärung: Wir können das Phänomen mit der Lorentzkraft beschreiben.
Kraft auf stromdurchflossenen Leiter
Wir wollen nun wissen, welche Kraft auf den Leiter wirkt. Dazu gehen wir von der Lorentzkraft aus:
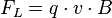
Wobei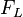 
die Lorentzkraft, 
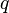die Ladung, 
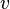die Geschwindigkeit der Teilchen und 
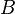die Stärke des Magnetfeldes angibt.
Betrachten wir unseren stromdurchflossenen Leiter, so wissen wir, dass sich darin die Elektronen mit einer Ladung von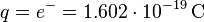 
bewegen. Jedoch können wir die Geschwindigkeit noch nicht direkt angeben.
Nach der Definition der elektrischen Stromstärke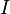 
gibt diese an, welche Ladungsmenge in einer bestimmten Zeit durch einen Leiter fließt. Es gilt also:
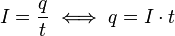
Für die Geschwindigkeit kennen wir aus der Mechanik den Zusammenhang
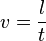
mit der Strecke bzw. der Leiterlänge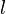 
und der Zeit 
.
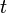Setzen wir diese beiden Zusammenhänge in die Formel für die Lorentzkraft ein so erhalten wir:
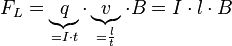
Auf einen Leiter der Länge 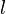in einem Magnetfeld 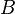wirkt bei einer Stromstärke 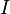also die Kraft
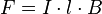
Aufgabe 1
Das magnetische Feld eines Dauermagneten in einem Drehspulinstrument besitzt die magnetische Flussdichte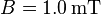 
. Auf ein zu diesem Magnetfeld senkrechtes Leiterstück der Länge 
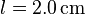wirkt die Kraft 
.
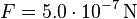Wie groß ist die elektrische Stromstärke ?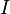
Lösung
gegeben: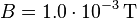 
, 
,
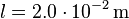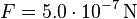
gesucht: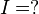 
Formel umstellen: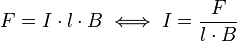 
einsetzen: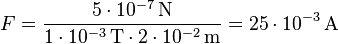 
Antwort: Durch den Leiter fließt eine Stromstärke von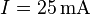 
Aufgabe 2
In einem Magnetfeld befindet sich ein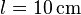 
langer elektrischer Leiter. Auf diesen wirkt eine Kraft von 
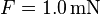. Die elektrische Stromstärke beträgt <ath>I=3.0\,\mathrm A</math>.
- Wie groß ist die magnetische Flussdichte Fehler beim Parsen (Lexikalischer Fehler):
beträgt?
Lösung 1
gegeben: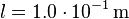 
, 
, 
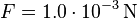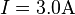
gesucht: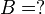 
Formel umstellen: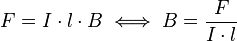 
einsetzen und ausrechnen ergibt: Die magnetische Flussdichte beträgt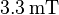 
Lösung 2
Zerlegung der Länge im Magnetfeld
Ist der Leiter nicht senkrecht zum Magnetfeld, so müssen wir zunächst die vektorielle Geschwindigkeit zerlegen. Die Lorentzkraft wirkt nämlich nur auf den Anteil, der senkrecht zum Magnetfeld steht. Die wirksame Länge - also diejenige, die senkrecht zum Magnetfeld steht - berechnet sich aus der Länge multipliziert mit dem Sinus des Winkels:
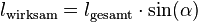
Für die Kraft auf einen schräg im Magnetfeld liegenden Leiter gilt also:
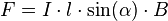
Anmerkung: natürlich gilt diese Formel immer, da bei einem senkrechten Leiter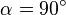 
und damit 
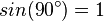gilt.
Zur Lösung der Aufgabe müssen wir also lediglich diese Formel verwenden:
gegeben: , , ,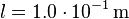 
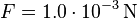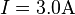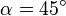
gesucht: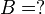
Formel umstellen: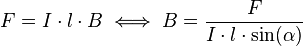 
einsetzen und ausrechnen ergibt: Die magnetische Flussdichte beträgt 
