Abstand Punkt-Gerade

Vorwissen

Vektoren, Skalarprodukt, Geraden im Raum, Ebenen im Raum, Normalenvektor, Schnittpunkt Gerade-Ebene

Problem

Wir haben eine Gerade 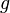im Raum und einen Punkt 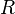welcher nicht auf der Geraden liegt. Wir können bisher noch keinen Abstand zwischen Punkt und Gerade berechnen.

Beispielsweise spielt der Abstand bei Planung eines Flughafens eine Rolle, denn hier können die Bahnen der startenden und landenden Flugzeuge als Gerade angenähert werden. Dabei muss immer ein gewisser minimaler Sicherheitsabstand zu umliegenden Gebäuden eingehalten werden.

Erinnerung

In einer früheren Klasse wurde das Problem bereits im zweidimensionalen behandelt. Hier wurde der Abstand gemessen indem das Geodreieck orthogonal so auf die Gerade gelegt wurde dass der Punkt auf der Skala liegt. Dann konnte der Abstand rechtwinklig am Geodreieck abgelesen werden.

Animation

Um das Problem eines startenden Flugzeugs zu verdeutlichen gibt es folgende Animation. Das Flugzeug kann dabei an der unteren Ecke entlang der Geraden verschoben werden:

Aufgrund der Problemstellung, dass ein minimaler Sicherheitsabstand eingehalten werden muss ergibt sich folgende Definition.

Definition

Als Abstand zwischen einer Geraden 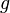und einem Punkt 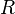ist definiert als kleinstmöglicher Abstand zwischen diesen beiden.

formell

Eine Gerade ist definiert als Punktmenge (mit 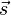: Stützvektor und 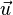: Richtungsvektor, vgl. Geraden im Raum):

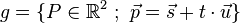
dann gilt für den Abstand

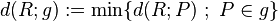
Folgerung

Wie wir in der Animation auch anschaulich erkennen können, ist dieser minimale Abstand gerade dann gegeben, wenn der Verbindungsvektor 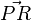orthogonal zur Geraden, bzw. deren Richtungsvektor 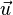steht, d.h. das Skalarprodukt Null ergibt.

formeller Beweis

Diese Folgerung kann auch mathematisch mit dem Skalarprodukt bewiesen werden:

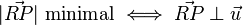
Hier soll jedoch nur die 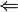-Richtung gezeigt werden, welches der Behauptung entspricht: ist 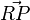orthogonal zu 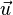, dann ist 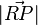minimal.

Wir wählen uns also den Punkt 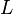gerade so, dass 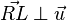gilt. Zu zeigen ist nun, dass gerade der Abstand 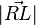der kürzestmögliche ist. Dazu wählen wir einen beliebigen Punkt 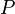auf der Gerade und beweisen, dass 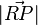immer größer ist als 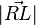(für ).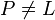

Ohne Einschränkung nehmen wir an, dass 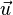bereits ein Einheitsvektor ist (ansonsten können wir diesen zuerst normalisieren, da die Länge des Richtungsvektors für die Gerade keine Rolle spielt). Mit der formellen Definition des Skalarproduktes wissen wir:

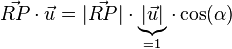
Außerdem gilt

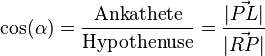
Durch Einsetzen erhalten wir:

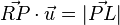
Daraus können wir folgern: ist 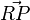orthogonal zu 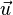, so ist das Skalarprodukt und damit .

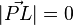Der Rest kann nun mit dem Satz von Pythagoras gefolgert werden, denn es gilt:

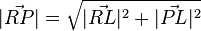
Da 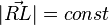(da beide Punkte fest sind) wird das Minimum von 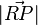gerade dann erreicht, wenn 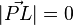ist. Hier gilt dann aber, wie oben gezeigt, dass 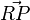orthogonal zu 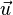ist. Das bedeutet: das Minimum von 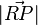ist genau dann gegeben, wenn 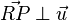gilt! q.e.d.